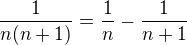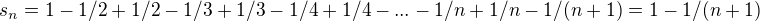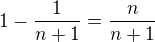Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 27. 09. 2014 21:30 — Editoval binuralka (27. 09. 2014 21:39)
řady
Dobrý den,
potřeboval bych poradit s těmito úlohami:
1: Mezi každé dva členy nekonečné konvergentní geometrické řady 1 + a + a^2 + a^3 + .... je vlozen dalsi clen tak, ze spolu s puvodnimi cleny tvori opet nekonecnou konvergentni geometrickou radu. Urci soucty obou rad a stanov, pro ktera a (z realnych cisel) je tato rada konvergentni.
2: Dokaz ze rada [suma - nahore nekonecno, dole n=1] 1/n*(n+1) je konvergentni. Stanov jeji soucet.
Děkuji předem za čas.
Offline
#2 27. 09. 2014 21:44 — Editoval Arabela (27. 09. 2014 21:46)
Re: řady
↑ binuralka:
Ahoj, k druhému príkladu. Skús ukázať, že 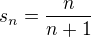 . Potom bude už ľahké vypočítať príslušnú limitu...
. Potom bude už ľahké vypočítať príslušnú limitu...
server.gphmi.sk/~domanyov
Offline
#3 27. 09. 2014 21:47
Re: řady
↑ binuralka:
1: Pro každé tři po sobě jdoucí členy GP platí 
Pak pro  ,
, 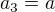 bude
bude 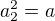
a to by ti mělo stačit
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#4 27. 09. 2014 22:01 — Editoval binuralka (27. 09. 2014 22:02)
Re: řady
Arabela napsal(a):
↑ binuralka:
Ahoj, k druhému príkladu. Skús ukázať, že. Potom bude už ľahké vypočítať príslušnú limitu...
Proc jsi pouzila prave tento vzorecek? Pokud budu chtit spocitat posloupnost částečných součtů o dvou clenech (a1 + a2) podle tveho vzorecku, tak mi vyjde 2/3, ale pokud si opravdu sectes a1, a2..tak dostanes = 4/3
Offline
#5 27. 09. 2014 22:07
Offline
#6 27. 09. 2014 22:09
Offline
#7 27. 09. 2014 22:29
Re: řady
nevím jak postupovat... co si přečíst, nastudovat?
zde, je přesné zadání: https://www.dropbox.com/s/9dlr4bssnwqhr … 222611.jpg
Offline
#8 27. 09. 2014 22:34
Re: řady
↑ binuralka:áno, takže ten druhý príklad je tak, ako som ho pochopila...
Postupnosť čiastočných súčtov teda je 
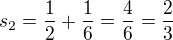

atď. ...
server.gphmi.sk/~domanyov
Offline
#9 27. 09. 2014 22:40
Re: řady
↑ Arabela:
ano, pardon, dopustil jsem se hloupe pocetni chyby. jak jsi prisla, jaky je postup? na Sn= n/(n+1) ?
Offline
#10 27. 09. 2014 22:51
Re: řady
↑ binuralka:spomenula som si, ako nám to kedysi ukázali v škole - bol v tom taký trik... Kolega zdenek1 ho už vlastne naznačil... V tom nekonečnom súčte si každý člen rozpíšeme ako onen rozdiel, takže dostaneme .
.
Teraz si všimneme, že počnć druhým členom sa vždy dva susedné členy rušia... vidíš to?
server.gphmi.sk/~domanyov
Offline
#11 27. 09. 2014 22:57
Re: řady
↑ Arabela:
ano, vidim...
Sn = 1 - 1/2 - 1/3 - 1/4... -1/n
a dal... jak dostaneme tu formu n/(n+1)
Offline
#14 27. 09. 2014 23:13
Offline


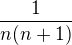 ?
?