Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 28. 09. 2014 10:46
#6 28. 09. 2014 10:55
Re: Počítání s faktoriály
↑ mates.dz:Díky,postup sem měl stejný,jenom mě nenapadlo to podělit,nebo vytknout,hledal jsem v tom zbytečné složitosti :-). Jinak díky za vysvětlení.
Offline

 a nějak nevím co s tím,můžete mi prosím poradit?
a nějak nevím co s tím,můžete mi prosím poradit?![kopírovat do textarea $n\cdot(n!+(n-1)!)=(n+1)!=n[n(n-1)!+(n-1)!]$](/mathtex/8e/8ec42540f57d5a54bcf5746cb67fdaff.gif) a vytkneš
a vytkneš 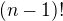 před závorku
před závorku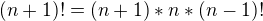


 .
.