Matematické Fórum

Opulentus · 29. 09. 2014 19:07

Dobrý den,
mám načrtnout graf funkce $log_{2}|x|$ . Nevím si moc rady...
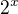Myslím, že to bude inverzní funkce k $2^{x}=|y|$ a jelikož $2^{x}$ nemůže nýt záporné (tedy myslím), je tam absolutní hodnota "zbytečná"? (V Wolfram aplha ale mají k funkci $log_{2}|x|$ graf: //forum.matweb.cz/upload3/img/2014-09/10386_V%25C3%25BDst%25C5%2599i%25C5%25BEek.PNG
tak nevím, jak na to.

Předem díky za rady...

Bati · 29. 09. 2014 19:13

↑ Opulentus:
Ahoj,
inverzní funkci tady moc nepotřebuješ.
Zkus si odpovědět na tyto otázky:
1) Jaký je definiční obor logaritmu?
2) Co můžeš říct o sudosti/lichosti dané funkce?
Pak by už mělo být jasné jak udělat graf.

mates.dz · 29. 09. 2014 19:14

Ta absolutna hodnota neni zanedbatelna sprav graf pre kladne cisla a vies ze teraz je parna takze ju iba dorob zrkadlovo podla osi y

misaH · 29. 09. 2014 20:26

↑ Opulentus:

Tá absolútna hodnota znamená, že môžeš dosádzať aj záporné hodnoty x, čo sa bez AH v argumente nedá.

Ako píšu kolegovia predo mnou, graf je potom súmerný podľa osi y, lebo funkcia s AH je párna (f (x)=f (-x)).

Opulentus · 29. 09. 2014 20:44

Jestli to tedy správně chápu, říká mi to, že mohu dosadit za x i záporné číslo a funkce mi dá to samé, jako pro stejné nezáporné číslo?

A ještě jeden dotaz, mohu mít funkci $-(log_{a}x)$ , která by pak vypadala, pro a větší než 1, jako stejná funkce, pro a menší než 1, nebo to takhle nelze udělat?

Bati · 29. 09. 2014 21:05

↑ Opulentus:
V první části tvé otázky jsi popsal absolutní hodnotu.

Ke druhé části:
$-\log_a x=-\frac{\log x}{\log a}=\frac{\log x}{\log\tfrac1a}=\log_{\frac1a}x$ .

Opulentus · 29. 09. 2014 21:28

Díky moc!!

A můžete mi ještě prosím poradit , jak se vyřešit tuto úlohu: Najděte množinu všech bodů (x,y) pro které zároveň platí: $y > log_{2}x$ , $y<4^{x}$ , $x\le 1$ , $y> -x-2$
Vyšlo mi, že z první podmínky budou všechny souřadnice y větší než nula. Takže všechny body budou mít souřadnici x 1 a souřadnice y budou (0,4).

Ale asi to mám špatně- v logaritmech mám nějaký zmatek...

misaH · 29. 09. 2014 22:04 — Editoval misaH (29. 09. 2014 22:07)

↑ Opulentus:

$y > 0$

To asi nie

Ak $x=\frac 12, \text {tak} y=-1$

Vychádzaj z grafov daných funkcií, ak ich nepoznáš, niekde ich vyhľadaj.

Začala by som s poslednými dvoma.

zdenek1 · 29. 09. 2014 22:07

↑ Opulentus:
//forum.matweb.cz/upload3/img/2014-09/21199_graph.png

Tady máš hranice

Bati · 29. 09. 2014 22:25 — Editoval Bati (29. 09. 2014 22:27)

↑ Opulentus:
Začni xovou souřadnicí- kvůli 3. podmínce a první (def. obor logaritmu) musí být $x\in(0,1]$ . Dále na tomto intervalu bude třeba načrtnout grafy funkcí daných 1., 2. a 4. podmínkou (což udělal zdeněk) a zjistit, kde se protínají. Pak už to bude snadné.

Jen bych ještě poznamenal, že zadání "Najděte množinu všech bodů, pro které platí ..." je docela smutně formulované, protože takové zadání je zároveň odpovědí. Jde tedy asi spíš o ňejaké zjednodušení daných podmínek.

Eratosthenes · 29. 09. 2014 23:37

ahoj ↑ Opulentus:,

graf každé funkce f(|x|) dostaneš z grafu funkce f(x) tak, že vezmeš graf funkce f(x), v případě potřeby omezíš definiční obor na nezáporná čísla (což u logaritmu samozřejmě dělat nemusíš) a k tomuto grafu připojíš graf symetrický podle osy y. V tomto konkrétním případě vezmeš graf log_2(x) a k němu sestrojíš ještě křivku symetrickou podle osy y tak, jak to máš na svých obrázcích. Omezovat nic nesmíš, definičním oborem této funkce je množina R-{0}. Např. log_2(|-1024|)=log_2(1024)=10.

Opulentus · 30. 09. 2014 17:08

Díky všem za odpovědi!!
Jenom mi to pořád asi trochu nedochází...

Chápu to tedy správně, že je to množina všech těchto bodů? //forum.matweb.cz/upload3/img/2014-09/89645_21199_graph.png

zdenek1 · 30. 09. 2014 17:16

↑ Opulentus:
Ano. plus hranice i x=1

Opulentus · 30. 09. 2014 21:20

Díky moc všem!!

Matematické Fórum

#1 29. 09. 2014 19:07

Logaritmus - absolutní hodnota

#2 29. 09. 2014 19:13

Re: Logaritmus - absolutní hodnota

#3 29. 09. 2014 19:14

Re: Logaritmus - absolutní hodnota

#4 29. 09. 2014 20:26

Re: Logaritmus - absolutní hodnota

#5 29. 09. 2014 20:44

Re: Logaritmus - absolutní hodnota

#6 29. 09. 2014 21:05

Re: Logaritmus - absolutní hodnota

#7 29. 09. 2014 21:28

Re: Logaritmus - absolutní hodnota

#8 29. 09. 2014 22:04 — Editoval misaH (29. 09. 2014 22:07)

Re: Logaritmus - absolutní hodnota

#9 29. 09. 2014 22:07

Re: Logaritmus - absolutní hodnota

#10 29. 09. 2014 22:25 — Editoval Bati (29. 09. 2014 22:27)

Re: Logaritmus - absolutní hodnota

#11 29. 09. 2014 23:37

Re: Logaritmus - absolutní hodnota

#12 30. 09. 2014 17:08

Re: Logaritmus - absolutní hodnota

#13 30. 09. 2014 17:16

Re: Logaritmus - absolutní hodnota

#14 30. 09. 2014 21:20

Re: Logaritmus - absolutní hodnota

Zápatí