Matematické Fórum

myrek · 30. 09. 2014 20:54

dobry den
zadani prikladu:
necht 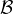$\mathcal{B}$ je podprostorem afinniho prostoru $\mathcal{A}$ .
Urcete zda bod lezi v podprostoru 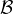$\mathcal{B}$ , jestlize
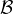$\mathcal{B}$ ≡ [1,5,9] +k(3,5,7) +l(4,6,8) ; k,l realna
bod[-4,0,4]

moc nevim jak postupovat, pocita se to takto?
[-4,0,4]=[1,5,9] +k(3,5,7) +l(4,6,8)
[-5,-5,-5]=(3k+4l,5k+6l,7k+8l)
3k+4l=-5, 5k+6l=-5, 7k+8l=-5
...

nebo se postupuje jinak, diky za navod

vanok · 30. 09. 2014 21:34

Akoj ↑ myrek:,
Tvoja metoda sa da pouzit na dane cvicenie.
Iste si ukazal ze k+l=0.
Tak to vyuzi.

myrek · 30. 09. 2014 22:28

↑ vanok:
tak ja dostal primo k=5,l=-5
takze kdyz je reseni tak bod lezi vpodprostoru
a kdyz neexistuje reseni tak tam nelezi?

vanok · 30. 09. 2014 22:29

↑ myrek:
Presne tak.

myrek · 30. 09. 2014 22:53

↑ vanok:
diky za kontrolu

a jeste mam jeden priklad a u toho nevim vubec postup

urcete, ktera z podmnozin je zaroven i podprostorem afinniho prostoru
$\mathcal{A}$ = $R^3$
a) {[7,5,4]+k(4,7,1) | 0≤k≤10}
b) {[0,0,4]}
c) $\{[x_1,x_2,x_3] A | x_1,x_2,x_3 \in R, x_3=3 nebo x_3=2\}$

vanok · 01. 10. 2014 00:04

Ahoj ↑ myrek:,
Bez tvojich materialov je mi tazko odpovedat. Posli URL. Dakujem

vanok · 01. 10. 2014 00:27 — Editoval vanok (01. 10. 2014 00:27)

Ahoj ↑ myrek:,

Inac sa mi zda z 3 situacii, jediny co vyhovuje je b) ide o priestor ktoreho reper ma pociatok v bode [0,4,4] a asociovany vektorovy priestor je nulovy.
( ale neviem aku terminologiu pouzivate vo vasich marerialoch)

Eratosthenes

ahoj ↑ myrek:,

Jediným "kandidátem" je b) (byl by to tzv. triviální podprostor). Ale jak pravil kolega ↑ vanok:, záleží na tom, jak máte definován afinní prostor. Pokud algebraicky, je to OK. Ale já bych obhájil i tvrzení, že b) podprostorem není. Afinní prostor lze totiž definovat i podle geometrických axiomů (je to "běžný" prostor, ze kterého vyloučíme axiomy shodnosti). V tom případě ovšem podle jednoho axiomu incidence musejí v tom prostoru ležýet alespoň tři body...

myrek · 01. 10. 2014 16:55

↑ vanok:↑ Eratosthenes:
posilam odkaz
http://www.math.muni.cz/~janyska/AFPR-H.pdf

aha raper tak to jsme jeste moc neprocvicili

Eratosthenes · 01. 10. 2014 17:04

↑ myrek:

takže definice jasná => b) je OK.

vanok · 01. 10. 2014 17:20 — Editoval vanok (01. 10. 2014 17:29)

↑ Eratosthenes:,
Ano uplne suhlasim.
Pretoze sa v pouzitych materialoch jedna o realne priestory ( ako aj na strednych skolach ) je mozne intuitive v nich pracovat.

Matematické Fórum

#1 30. 09. 2014 20:54

afinni podprostor

#2 30. 09. 2014 21:34

Re: afinni podprostor

#3 30. 09. 2014 22:28

Re: afinni podprostor

#4 30. 09. 2014 22:29

Re: afinni podprostor

#5 30. 09. 2014 22:53

Re: afinni podprostor

#6 01. 10. 2014 00:04

Re: afinni podprostor

#7 01. 10. 2014 00:27 — Editoval vanok (01. 10. 2014 00:27)

Re: afinni podprostor

#8 01. 10. 2014 16:51 — Editoval Eratosthenes (01. 10. 2014 17:02)

Re: afinni podprostor

#9 01. 10. 2014 16:55

Re: afinni podprostor

#10 01. 10. 2014 17:04

Re: afinni podprostor

#11 01. 10. 2014 17:20 — Editoval vanok (01. 10. 2014 17:29)

Re: afinni podprostor

Zápatí