Matematické Fórum

petacv · 01. 10. 2014 19:00

Je dána posloupnost

$a_{n+1}=\frac{1}{2}\langle a_{n}+\frac{2}{a_{n}}\rangle , a_{1}=1$

Pro dostatečně vysoké n se $a_{n\approx \sqrt{2}}$

1. změním-li 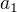$a_{1}$ bude stále platit $a_{n\approx }\sqrt{2}$ ?
2. je tímto způsobem možno spočítat i jinou odmocninu, např. 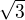$\sqrt{3}$ ? Co se musí změnit v zadání?
3 mohu výpočet libovolně zpřesňovat ?

Tak již mi chybí tento příklad a nevím si s tím rady. Prosím chytré hlavičky o pomoc, děkuji. Nevím jak na postup

Bati · 01. 10. 2014 19:26

Ahoj,
znalost Newtonovy metody tečen ti dá odpověď na všechny tvoje otázky.

petacv · 01. 10. 2014 22:25

↑ Bati:

nedám to :-(

Marian · 03. 10. 2014 08:20

↑ petacv:

Jedná se o tzv. Heronovo odmocňování (někdy též babylonské odmocňování). K zodpovězení tvých otázek je naprosto zbytečné studovat Newtonovu metodu zmíněnou výše. Jedná se o základní (avšak komplexní) problém z oblasti rekurentně daných posloupností. Dle mého názoru je velmi vhodné řešit elementární matematické problémy elementárními technikami, které plně postačí (pojmu derivace, kontraktivního zobrazení nebo BPPB skutečně nebude potřeba, i když tyto věci značně souvisí).

ad 1. Změním-li startovací hodnotu na jinou kladnou, hodnota limitní hodnoty se nezmění. Zvolím-li zápornou startovací hodnotu, posloupnost bude konvergovat k hodnotě $-\sqrt{2}$ .

ad 2. Uvedeným způsobem je možno spočítat i odmocninu 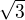$\sqrt{3}$ tak, že změníme rekurentní vztah na

ad 3. Výpočet je možno libovolně zpřesňovat výpočtem členů $a_n$ s dostatečně vysokým indexem $n$ . Zhruba platí, že výpočtem každého dalšího členu zdvojnásobím počet korektních desetinných míst.

Ovšem tyto závěry je nutno podložit nějakými vysvětleními, nejlépe důkazem. Takový důkaz však nevyužívá (ve všech výše uvedených bodech) ničeho jiného, než vlastností omezených monotónních posloupností.

Věřím, že můj plytký komentář v tuto chvíli postačí.

Matematické Fórum

#1 01. 10. 2014 19:00

Posloupnost an+1

#2 01. 10. 2014 19:26

Re: Posloupnost an+1

#3 01. 10. 2014 22:25

Re: Posloupnost an+1

#4 03. 10. 2014 08:20

Re: Posloupnost an+1

Zápatí