Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Inverzní funkce k funkci s absolutními hodnotami (TOTO TÉMA JE VYŘEŠENÉ)
#2 05. 10. 2014 14:30 — Editoval Sulfan (05. 10. 2014 14:31)
Re: Inverzní funkce k funkci s absolutními hodnotami
Ahoj, máš to skoro celé dobře, jen ses upsal v případě 
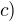 , kde jsi řešil rovnici
, kde jsi řešil rovnici 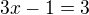 , která má na intervalu
, která má na intervalu  řešení
řešení 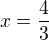 . Celkem je tedy řešení
. Celkem je tedy řešení 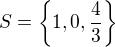 .
.
EDIT: Aby byla řešením množina, kterou mají ve výsledcích, musela by v zadání být množina  .
.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Inverzní funkce k funkci s absolutními hodnotami (TOTO TÉMA JE VYŘEŠENÉ)

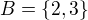
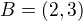 ->
-> 
 ->
-> 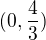
 ->
-> 
 ->
->