Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 24. 02. 2009 23:19
Několik příkladů...
Zdravim, počítal jsem si něklik příkladů a pokud by mi je někdo mohl zkontrolovat, případně přidat nějaký komentář k řešení, snažší cestu atd. budu moc rád. Děkuji Vám předem.
1.) Číslo  je rovno číslu? (je to logaritmus o základu 5, aby nedošlo k omylu)
je rovno číslu? (je to logaritmus o základu 5, aby nedošlo k omylu)


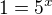

2.) 
3.) 


4.) V geometrické posloupnosti znáte:

Zjistěte  ...
... 


5.) V rovině jsou dány body A = [-1,2] , B = [m,3] a C = [1,-4], kde m je reálný paramter. Hodnota perametru m, pro kterou jsou přímky AB a AC kolmé je roven číslu?




6.) je dána kružnice  určete poloměr.
určete poloměr.

*********
Rád bych pokračoval zítra dalšími příklady, pokud se zde najde někdo, komu nevadí mi je opravit. Děkuji Vám a přeji dobrou noc!
Offline
#2 24. 02. 2009 23:28
Re: Několik příkladů...
↑ joker:
Normálne radosť čítať :) Keby si to každý takto dôkladne pripravil alebo sa pýtal na konkrétne veci, bol by som spokojný. Myslím, že tam nie sú chyby ako som to prebehol.
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
