Matematické Fórum

byk7 · 08. 10. 2014 07:45

V rovině je dána osa 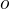$o$ a v navzájem opačných (otevřených) polorovinách jsou dány body $A$ a $A'$ . Geometricky určete body $S$ , $F$ a $V$ dutého zrcadla, které zobrazuje $A$ na $A'$ .

jelena · 08. 10. 2014 10:45

Zdravím,

inspiroval Tebe pohled do nerez misky u snídaně a máš zajímavou úlohu? Potom to patří tam (a dle vzoru kolegy, co skákal v bazénu, prosím o motivační úvod :-)) Děkuji.

byk7 · 08. 10. 2014 11:16

Zdravím,

ne, inspiroval mě profesorka fyziky a zadala tuto úlohu. :-)
Pokoušel jsem se ji vyřešit a našel jsem tam pár podobných trojúhelníků,
ale pořád je to málo...

jelena · 08. 10. 2014 17:05 — Editoval jelena (08. 10. 2014 17:06)

↑ byk7:

děkuji. Bod S, předpokládám, jsi našel, dostupné rovnoběžky nakreslil. Východní zdroje povídají toto (klíčová je úsečka ab, bd). Ale proč to platí, to teď neřeknu.

Do Zajímavých přesunu (zpět nevím - asi ne, neboť v sekci Zajímavé Fyziky nemám žádná práva, což mi neumožňuje umístit zvýrazněné vstupní téma :-) Edit - přesunul kolega Zdeněk, děkuji a pozdrav.

byk7 · 08. 10. 2014 17:54

↑ jelena:

Co je za body a,b,d? A co je bod P? A jak dostanu K?
Ze zdroje mi to není vůbec jasné.

jelena · 08. 10. 2014 20:17

↑ byk7:

Ze zdroje mi to není vůbec jasné.

pokud jde o ruštinu, tak naše škola má pobočku i v Brně :-) Ale pokud jde o fyzikální smysl, tak mi to také není jasné, co podnikali a proč, ale popíší, pokud bude zájem.

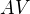Pokud budu uvažovat, že paprsek, který jde z bodu $A$ k vrcholu $V$ , tak se odrazí pod stejným úhlem, pod kterým dojde, tedy úsečka $AV$ se zobrazí v osové souměrnosti na 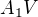$A_1V$ a měla bych pomocný bod 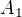$A_1$ na stejné polorovině jako $A'$ - snad se zorientujeme i v jiném označení - obr. 2.19.. Potom využiji, že střed křivosti je na spojnici bodů $A$ a $A'$ atd. Tak teď mám dojem, že údajů je snad i více, než potřeba.

Jak to vidíš?

byk7 · 08. 10. 2014 20:36

Aha... Takže, pochopil jsem to tak, že zobrazíme $A'\mapsto B$ podle osy $o$ a průsečík přímky $AB$ a osy $o$ bude $V$ ?

jelena · 08. 10. 2014 20:43

↑ byk7:

také bych to tak viděla.

byk7 · 08. 10. 2014 23:04

Tak jsem si s tím zkoušel hrát v Geogebře a řekl bych, že ↑ toto: neplatí.

jelena · 08. 10. 2014 23:43

↑ byk7:

užití osové souměrnosti neplatí? To je podle mne základní východisko u zrcadel. A odkdy se dokazuje obrázkem?

OT: učinila jsem drobné pokusy toto slepit, ale to se mi nepodařilo.

byk7 · 09. 10. 2014 00:15

↑ jelena:

Ah... já už vím, kde je chyba. Při odvození, nemýlím-li se, jsou použity nějaké aproximace, a ty se při vhodném nastavení projeví a vznikají chyby a nepřesnosti. Takže snad v pořádku.

jelena · 09. 10. 2014 10:09

↑ byk7:

tak to moc nevím, jak myslíš. Předpokládáme přímočaré šíření, v místě dopadu paprsku na plochu uděláme kolmici k ploše (v kulovém zrcadle tedy kolmici k tečné rovině v místě dopadu) a uvažujeme úhel odrazu = úhel dopadu.

V každém případě to, co podnikali ve východním odkazu, tak je mi záhadou :-)

byk7 · 09. 10. 2014 11:57

Jasné, to bylo jen noční zatmění mysli. :-)

Matematické Fórum

#1 08. 10. 2014 07:45

Geometrická konstrukce

#2 08. 10. 2014 10:45

Re: Geometrická konstrukce

#3 08. 10. 2014 11:16

Re: Geometrická konstrukce

#4 08. 10. 2014 17:05 — Editoval jelena (08. 10. 2014 17:06)

Re: Geometrická konstrukce

#5 08. 10. 2014 17:54

Re: Geometrická konstrukce

#6 08. 10. 2014 20:17

Re: Geometrická konstrukce

#7 08. 10. 2014 20:36

Re: Geometrická konstrukce

#8 08. 10. 2014 20:43

Re: Geometrická konstrukce

#9 08. 10. 2014 23:04

Re: Geometrická konstrukce

#10 08. 10. 2014 23:43

Re: Geometrická konstrukce

#11 09. 10. 2014 00:15

Re: Geometrická konstrukce

#12 09. 10. 2014 10:09

Re: Geometrická konstrukce

#13 09. 10. 2014 11:57

Re: Geometrická konstrukce

Zápatí