Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 12. 10. 2014 16:06 — Editoval Olínečka (12. 10. 2014 16:07)
Zatáčka - síla
Ahoj, potřebovala bych poradit s příkladem. Zatáčka o poloměru 30 m byla upravena skloněním povrchu vozovky o úhel 15°. Jak se tím zvýšila maximální bezpečně průjezdná rychlost vozidel, je-li součinitel tření pneumatik na vozovce 0,7? Má to vyjít 67,7 km/h.
Počítala jsem to tak, že jsem si vyjádřila síly, které na těleso působí - gravitační, třecí a dostředivá síla. Výsledná síla, která uvede těleso do pohybu bude F=Fd - Ft. Potom jsem udělala tangens alfa = F/Fg a nevyšlo to.
Díky za pomoc
Obrázek k tomu je tady: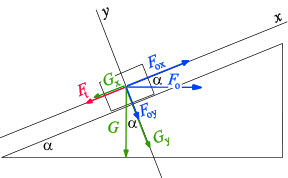
Offline
#2 12. 10. 2014 17:42
Re: Zatáčka - síla
a nevyšlo to.
A proč by taky mělo?
Aby těleso bylo ve směru  v rovnováze, musí platit
v rovnováze, musí platit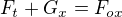
Je 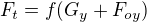
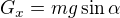
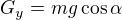
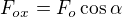
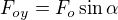
a 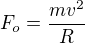
Zbytek jsou počty
Pořádek je pro blbce, inteligent zvládá chaos!
Offline