Matematické Fórum

Secren · 18. 10. 2014 12:19

Zdravím,
mám nasledujúcu úlohu:

Nechť M je množina všech podmnožin množiny přirozených čísel $\mathbb N$ a $(M, \subset)$ je její částečné uspořádaní inkluzí (tj. relací být podmnožinou). Má každá podmnožina $X\subset M$ v tomto uspořádání supremum?
V případech, že supremum existuje, popište, jak vypadá. Odpovědi zduvodněte.

Problém je že si nie som istý či platí v tomto usporiadaní pre podmnožinu $X\in M: X\subset X$ (reflexívnosť tejto relace).
Ak by to platilo tak supremum ľubovolnej podmnožiny M by bola mohla byť množina $S=\{x\in \mathbb N | \exists X\in M: x\in X \}$ ak sa nemýlim (buď by do tej množiny táto množina nepatrila alebo by bola najväčší prvok). Len si teraz niesom isty ci táto vlastnosť reflexívnosti platí v tomto zadaní (keby sa použilo $\subseteq$ tak by som si istý bol).

kompik · 18. 10. 2014 15:22

Zdá sa, že problém je hlavne v tom, že:
a) Niektoré knihy používajú 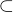$\subset$ na označenie podmnožiny, niektoré na označenia vlastnej podmnožiny.
b) Niektoré knihy pod pojmom čiastočné usporiadanie myslia neostré čiastočné usporiadanie, niektoré neostré čiastočné usporiadanie.
V oboch prípadoch je dôležité pre teba zrejme to, akú konvenciu máte na kurze, kde si toto zadanie dostal.

Ale bez ohľadu na to, akú konvenciu používate, suprémum vyzerá naozaj tak, ako si napísal.
A je to vlastne presne zjednotenie systému množín: $S=\bigcup M$ .

Matematické Fórum

#1 18. 10. 2014 12:19

Supremum podmnožiny všetkých podmnožín N

#2 18. 10. 2014 15:22

Re: Supremum podmnožiny všetkých podmnožín N

Zápatí