Matematické Fórum

Simon P40

mám zadán průměr a střední odchylku souboru:
$\overline{x} = 2.3$
$s_x = 0.3$

Z toho tedy chápu, že hodnoty se pohybují v intervalu $\langle1.8; 2.6\rangle$ (aspoň myslím)

Mám zjistit, jaký podíl hodnot přesáhne hodnotu 2.5

Jak na to? Díky

(jde o normální rozdělení)

OndrasV · 28. 10. 2014 06:44

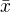↑ Simon P40: Ahoj, místo střední odchylka se říká směrodatná odchylka. Pokud není uveden počet pozorování a má to být normální rozdělení, tak $x \in (-\infty ,\infty )$ , byť velké hodnoty nabývá s velmi malou pravděpodobností. $Pr(X > 2.5) =1-Pr(X\le 2.5)$ . Tuto pravděpodobnost najdu v tabulkách normovaného normálního rozdělení, když od X odečtu $\bar{x}$ a podělím $s_{x}$ .

Simon P40 · 28. 10. 2014 11:30

Jo, směrodatná :)

částečně chápu, jen si nejsem jist tím koncem

$1-Pr(X\le 2.5) = 1-\Phi (2.5)$
hodnotu $\Phi (2.5)$ v tabulkách vidím. Co je ale to odečtení $\bar{x}$ a / $s_{x}$ ?
$(2.5-2.3)/0.3 = 2/3$ Co s tím? Díky

OndrasV · 28. 10. 2014 13:46

↑ Simon P40: Ne, ten konec je tak, že se používá $\Phi (2/3)$ , protože je to distr. fce normovaného normálního rozdělení.

Simon P40 · 28. 10. 2014 14:07

↑ OndrasV: ok, tak jen prosím, jaký je vztah mezi $Pr(X > 2.5) =1-Pr(X\le 2.5)$ a $(2.5-2.3)/0.3 = 2/3$

$Pr(X > 2.5) =1-Pr(X\le 2.5)$ chápu. Jaká je pravděpodobnost, že hodnoty jsou větší než 2.5 = 1 - (pravděpodobnost, že hodnoty jsou <= 2.5)

Ale proč se dělá tohle $(2.5-2.3)/0.3 = 2/3$ ? Díky moc

OndrasV · 28. 10. 2014 14:22

↑ Simon P40: Protože to 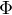$\Phi$ v tabulce je pro normované normální rozdělení, tj. s střední hodnotou $\mu = 0$ a směr. odchylkou $\sigma = 1$ . Ty máš normální rozdělení s stř. hodnotou 2,3 a směr. odchylkou 0,3, tak to na to normované normální rozdělení musíš převést, tedy od Y odečíst tu střední hodnotu a to celé podělit sm. odchylkou.