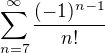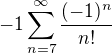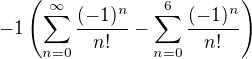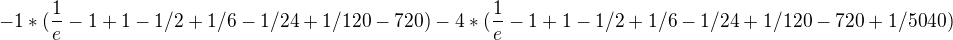Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#7 29. 10. 2014 19:46 — Editoval vizdo (29. 10. 2014 19:46)
Re: súčet radu
↑ Bati:
a ten prvý bude ako?
má to vyjsť toľkoto http://www.wolframalpha.com/input/?i=su … o+infinity
a mne vychádza to isté okrem čitateľa :(
Offline

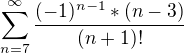
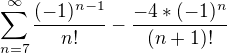
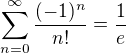 . Stačí to rozdělit na 2 sumy, přičíst a odečíst počáteční členy, případně posunout sčítací index.
. Stačí to rozdělit na 2 sumy, přičíst a odečíst počáteční členy, případně posunout sčítací index.