Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 03. 11. 2014 11:00
Teoretická mechanika
Ahojte, nevím si rady s tímto příkladem.
Prachová částice zanedbatelné hmotnosti padá v homogenním tíhovém poli skrz oblast nasycenou vodními parami. Páry na částici kondenzují tak, že hmotnost vznikající kapky vzroste na každém uraženém centimetru o  gramů. Najděte závislost uražené dráhy a rychlosti kapky na čase.
gramů. Najděte závislost uražené dráhy a rychlosti kapky na čase.
Prosím o pomoc :))
Offline
#2 03. 11. 2014 15:44 — Editoval Brzls (03. 11. 2014 17:52)
Re: Teoretická mechanika
↑ Renissh:
Čau
Pokud uvažujeme, že  se během pádu nemění, tak bychom mohli přistupovat takto.
se během pádu nemění, tak bychom mohli přistupovat takto.
Předpokládáme, že když pára kondenzuje na částici, tak při tom na ní nepůsobí žádnou silou. Dále zanedbáváme vztlakovou sílu (objem prachové částice je zanedbatelný a nezvětšuje se - pak by se měnilo i  )
)
Za těchto podmínek na částici působí pouze gravitační síla. Newtonův zákon říká
Jaký ještě dokážeme najít vztah mezi rychlostí a hmotností?
Dokážeš pokračovat?
Edit: Ty difky co mi z toho vylezly jsou celkem šílený, můžeš zkusit tipnout řešení ve tvaru polynomu ale když navíc uvážíš jaké údaje máš k dispozici tak na základě rozměrový analýzy můžeš určit řešení až na číselnou konstantu, kterou zjistíš zpětným dosazením do rovnic. Důkaz, že dané rovnice žádné jiné netriviální řešení nemají ke ale nad moje síly a divil bych se kdyby se to i požadovalo
Offline
#4 03. 11. 2014 22:40 — Editoval Brzls (03. 11. 2014 22:44)
Re: Teoretická mechanika
↑ Renissh:
No jasně že to z toho vyleze. No a co je pohybová rovnice? To je to co jsem psal
Když víš, že na každym centimetru přibude  gramů, tak jak závisí
gramů, tak jak závisí 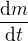 na rychlosti?
na rychlosti?
Tím dostaneš dvě rovnice ve kterých budeš mít hmotnost, rychlost a derivaci rychlosti. Vyluč z nich hmotnost, a základě rozměrový analýzy dosaď řešení ve tvaru  kde A je bezrozměrná konstanta a urči A.
kde A je bezrozměrná konstanta a urči A.
No a potom určit závislost dráhy na čase snad zvládneš.
Napiš kam až si se dostala.
Další varianta pokud nechceš s těmi rovnicemi dál pracovat je taková, že do nich rovnou dosadíš


a dostaneš dvě rovnice pro dvě neznámé A,B
Offline
#6 04. 11. 2014 08:23 — Editoval Brzls (04. 11. 2014 08:26)
Re: Teoretická mechanika
↑ Renissh:
Ok vidim ze k druhe rovnici si se dopracovala. Ty si ji resila pro drahu ja pro rychlost, proto ty rozdily v tvym postupu a v tom co jsem rikal.
Tu rovnici mas napsanou blbe ale kdyz tam dosazujes tak uz zase spravne takze predpokladam ze to je jen preklep. Pokud j to jen preklep tak je reseni spravne.
Vsimni si ze duvod proc je to umerne g*t na druhou je dusledek rozmerove analyzy. Ze zadanych udaju nelze jinou kombinaci dosahnout aby x melo rozmer metr a dokonce nelze zadnou kombinaci ani dostat bezrozmernou velicinu takze reseni opravdu nmuze byt jine. Kdyz to takhle zduvodnis muzes uplne automaticky predpokladat, ze x=Agt^2 . Pak samozrejme vyjde A=1/6.
Je to sice jen detail ale takhle aspon nikdo nemuze tvrdit ze sme to reseni proste jenom uhadli a navic i vidime zej jedine.
Jo a v poslednim radku kdyz pises v "case t=0" tak to radsi vynechej plati to pro libovolne t netreb dosazovat t=0
Offline


 . Počátá se přes pohybovou rovnici.
. Počátá se přes pohybovou rovnici.
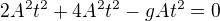
 a v čase t = 0
a v čase t = 0 