Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » nelineární rovnice (TOTO TÉMA JE VYŘEŠENÉ)
#2 08. 11. 2014 18:24
Re: nelineární rovnice
Ahoj ↑ aferon:
Napis cosh pomocou  a
a 
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 08. 11. 2014 18:45
Re: nelineární rovnice
Ako je definovany cosh x ?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 08. 11. 2014 19:04 — Editoval misaH (08. 11. 2014 19:05)
- misaH
- Příspěvky: 13460
Re: nelineární rovnice
↑ aferon:
Vanok chce od Teba definíciu.
http://sk.wikipedia.org/wiki/Hyperbolick%C3%A1_funkcia
Offline
#14 09. 11. 2014 14:02
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: nelineární rovnice
Zdravím,
jen drobnost - není nutné kolegu tlačit hned k použití vzorce. zde je na dobré cestě, jen dojit:
Teď bych řekl, že je teda obor hodnost cosh je od 1 do nekonečna a obor hodnost ex.fce je od 1do nekonečna, tudíž bod 5 je řešením ?
Máme součet funkcí  a víme, jaké minimální hodnoty mohou mít uvedené funkce, hledáme, pro které x to nastává (můžeme si pomáhat i grafickou metodou řešení rovnic). To "vytučnění" ještě není dobře.
a víme, jaké minimální hodnoty mohou mít uvedené funkce, hledáme, pro které x to nastává (můžeme si pomáhat i grafickou metodou řešení rovnic). To "vytučnění" ještě není dobře.
Ke vzorci - pozor, že argumentem cosh je (2x), oprav prosím (pokud není rovnou vidět, tak pomůže substituce 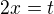 ).
).
Děkuji.
Offline
#18 09. 11. 2014 14:32
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: nelineární rovnice
↑ aferon:
děkuji, vzorec již dobře.
Stačí si nakreslit grafy funkce y= 3cosh(2x) a
a zjistit společný interval oborů hodnot?
Spíš si zakreslit grafy, jak jsi napsal, potom naznačit graf výsledného součtu (stačí, když si představíš, že hodnoty y pro stejné x stoji těsně vedle sebe jako 2 tyčky - pro každou funkci, v součtu tyčky postavíš na sebe). Méně polopaticky - určuješ obor hodnot až součtové funkce (což je nějaký interval). 5 napravo bude znázorněna při grafickém řešení jako přímka. Tedy můžeš odvodit, jak protne výsledný obor hodnot nalevo. Pokud prokážeš, že má jen jeden společný bod, potom zde hledáš řešení rovnice (obrázky zkus ve WA).
Offline
#20 09. 11. 2014 15:09
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: nelineární rovnice
↑ aferon:
výsledný graf je funkce nalevo v rovnici, napravo v rovnici je přímka y=5, technikou řešení je průsečík grafů (viz grafická metoda řešení rovnic). A tomu odpovídající hodnota na ose x (to je kořen rovnice).
Zakreslení součtového grafu - určitě umíš zakreslit graf y=f(x) a jeho různé transformace (viz transformace grafu), další práce - když máme 2 grafy, jejich součet zakreslíme pomocí postupného přenášení hodnoty pro jeden graf nad hodnotu pro 2. graf (například si to odzkoušej na y=x, y=2x+1 a y=(x)+(2x+1)). Stejně postupuješ i tady (zkus 3 grafy dat na jeden obrázek). Pokud bude fungovat - odkaz.
Prakticky bys měl umět odvodit obor hodnot i bez kreslení (a minimální hodnotu součtové funkce).
Offline
#21 09. 11. 2014 16:06
Re: nelineární rovnice
Tak nakreslil jsem si tu sčítanou funkci a ověřil jsem si to v programu, jak jste doporučila a už to chápu. Teď teda ale nevím, jak přijít na řešení. Mám udělat funkci y = 5 a sledovat, jestli mi protne to sčítanou funkci? Oborem hodnet je tedy <5;nekonečna)? podle grafu? a ten obor hodnot se dá vyčíst jen z grafu? nebo se dá i nějak vypočíst? Děkuji.
Offline
#22 09. 11. 2014 17:41
Re: nelineární rovnice
↑ aferon:
Teď jak se koukám i na jiný funkce, tak mi došlo, že vlastně obor hodnot nám ovlivňuje to, co zvyšuje nebo snižuje funkční hodnoty na ose y a to je vždy číslo, které násobí tu funkci a dále může dojít ještě k posunu po ose y, tak se ten obor hodnot taky upraví. Pak jak jste říkala sčítání těch grafů, tak to už si vlastně lze i představit.
Ale kdybych měl funkci třeba y=3(1+x)^(1/2) +5arcsin(2+x) tak tam už to půjde těžko sčítat a nakreslit sčítaný graf, zvlášť bez použití kalkulačky. Tak by to šlo nějak takhle?
obor hodnot arcsinx je 
obor hodnot 5arcsin(2+x) je 
obor hodnot y=3(1+x)^(1/2) je od <0;nekonečna>
takže výsledný obor hodnost funkce y=3(1+x)^(1/2) +5arcsin(2+x) je  ?
?
Offline
#23 09. 11. 2014 17:55
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: nelineární rovnice
↑ aferon:
vybav si ze SŠ grafické řešení rovnic (a nerovnic). Jak na řešení - reagovala jsem na to, že ve škole jste dělali obdobný postup pomocí oboru hodnot. Tak to mělo být podobné, za předpokladu, že si obor hodnot bez větších zádrhelů představíš.
Konkrétně v této úloze máme 2 funkce, co (z definice) jsou definovány na celém R, mají minimum a to dokonce pro stejné x=0. Tedy i součtová funkce bude definována na celém R a bude mít minimum pro stejné x=0. Obor hodnot vznikne tak, že minimální bod se posune výš po ose y, jinak do +oo to zůstává stejně.
Pro toto minimum můžeme přesně spočítat f(0)=5. A shodou okolnosti se nás ptají, pro které x platí, že  , tak jsme to všechno využili. Předchozí úvahy bychom mohli použit pro řešení
, tak jsme to všechno využili. Předchozí úvahy bychom mohli použit pro řešení  nebo pro stanovení počtu řešení
nebo pro stanovení počtu řešení  . Také pro řešení nerovnice můžeme použit.
. Také pro řešení nerovnice můžeme použit.
Tato metoda není univerzální, hodí se pro "pěkné zadání", kdy z vlastností funkcí je řešení "vidět".
Z náhledu:
3(1+x)^(1/2) +5arcsin(2+x)
tam pozor - zvolil jsi funkci, kde jsou zrádné def. obory pro jednotlivé sčítané, tedy i pro celou funkci (na druhou stranu to může být výhoda, pokud nic nezanedbáš při rozboru).
Principu metody rozumíš. Pokud takto (bez využití derivací) prozkoumáš více funkcí a jejích grafů, může to být užitečný základ pro další výpočty (zejména pro rychlé odhady). Navíc i Tobě bude jasné, že stavíš na pochopených teoretických základech (ne, že bych měla něco proti vzorci, co se navrhoval, ale věřím, že i kolega vanok potvrdí, že i takové zkoumání funkcí může být k užitku).
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » nelineární rovnice (TOTO TÉMA JE VYŘEŠENÉ)




 , že?
, že?

 teď substituci zpět. Ale neztrácej naději dojit přes obory hodnot :-)
teď substituci zpět. Ale neztrácej naději dojit přes obory hodnot :-)

