Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Derivace maticových výrazů (TOTO TÉMA JE VYŘEŠENÉ)
#1 08. 11. 2014 16:12 — Editoval Neth (08. 11. 2014 18:37)
Derivace maticových výrazů
Zdravím všechny, píšu sem kvůli následujícímu.
Mám problém si představit některé derivace maticových výrazů a to bohužel naprosto intuitivně jasných. Když si třeba vezmu zobrazení  ,
,  , kde
, kde  a
a  . Intuitivně mi přijde jasný, že derivace bude
. Intuitivně mi přijde jasný, že derivace bude  , ale pokud si to rozepíšu po složkách, už mi to vůbec není tak jasné a přijde mi, že se musí vynulovat všechny prvky matice kromě diagonály...
, ale pokud si to rozepíšu po složkách, už mi to vůbec není tak jasné a přijde mi, že se musí vynulovat všechny prvky matice kromě diagonály...
Chápu, že je tohle asi hodně hloupý dotaz, ale byl by někdo, prosím, tak hodný a poradil mi? Děkuju.
EDIT:
Na toto jsem už přišla, zasekla jsem se však na další související věci: Pokud mám zobrazení  a
a  , kde
, kde  , jaký je nejlepší způsob jak dokázat, že derivace f je
, jaký je nejlepší způsob jak dokázat, že derivace f je  ? Předem moc děkuju za odpověď.
? Předem moc děkuju za odpověď.
Offline
- (téma jako vyřešené označil(a) Neth)
#2 10. 11. 2014 12:33
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Derivace maticových výrazů
Zdravím,
další související věci:
nepomůže tomu, dívat se na výchozí krok jako na derivaci součinu  ? Děkuji (a přesunu dle pokynu).
? Děkuji (a přesunu dle pokynu).
Offline
#4 10. 11. 2014 21:03
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Derivace maticových výrazů
↑ Neth:
já jsem to zkoušela rozepsat jako řádek g_1(x), g_2(x)...g_n(x) a k tomu sloupec (podobně), jelikož po vynásobení jsou členy (g_1(x))^2 ..., tak derivace (s ohledem, že funkce g(x) je složená) vychází, jak požaduješ, ale tak to asi nechceš odvozovat.
To jsi odvozovala jak? Děkuji.
Offline
#11 12. 11. 2014 15:37
Re: Derivace maticových výrazů
↑ Rumburak:
Parádnost, děkuji moc. Už mi to je všechno jasné.
Děkuju za čas vás všech.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Derivace maticových výrazů (TOTO TÉMA JE VYŘEŠENÉ)

 a jsem prakticky tam, kde jsem byla. Myslím, že by se mělo vycházet z
a jsem prakticky tam, kde jsem byla. Myslím, že by se mělo vycházet z ![kopírovat do textarea $[\textbf{x}^T\textbf{x}]'= 2\textbf{x}^T$](/mathtex/65/6593c3bff7b977262190a09ac7ffcf09.gif) a z derivace složené funkce, ale nemůžu přijít na to, jak to na to "naroubovat".
a z derivace složené funkce, ale nemůžu přijít na to, jak to na to "naroubovat".
 a
a  totéž?
totéž?

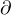 , je to i tady v editoru, hned první blok
, je to i tady v editoru, hned první blok , dále
, dále  .
. 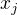 dostáváme
dostáváme ,
,