Matematické Fórum

Brzls · 13. 11. 2014 22:01

Zdravím

Je nějak obecně řešitelný tento problém? Slovem řešitelný myslím, jestli lze požadavek minimalizace převést na nějakou soustavu rovnic (prostě něco ve stylu Euler-Lagrangeovy rovnice) nebo tak něco.

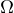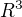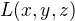Nechť $\Omega$ je nějaká souvislá oblast v $R^{3}$ a $L{(x,y,z)}$ je zadaná funkce souřadnic. Předpokládáme že tato funkce má "pěkné" vlastnosti (spojitost, spojitost a existence všech derivací-jeli to potřeba atd.)

Pokud platí
$\int_{\Omega }^{}d^{3}x=V$ kde V je pevně zadané reálné číslo, tak najděte takovou oblast omega, pro kterou má integrál

$I=\int_{\Omega }^{}L{(x,y,z)}d^{3}x$

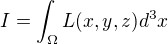
minimální hodnotu.
Taky víme, že oblast omega musí obsahovat bod (0,0,0)

Chtěl jsem si na toto téma něco najít a přečíst, ale pak sem zjistil, že ani nevím pod jakým heslem vyhledávat, tak se ptám zde. Navíc se mi zdá, že to je dost specifický problém o kterém se v základních textech o variačním počtu nemluví, tak to dávám do této sekce, jestli to sem nepatří tak klidně přesuňte.
Děkuji za jakoukoli reakci

Rumburak · 14. 11. 2014 11:11

↑ Brzls:

Také zdravím.

Rozumím úloze takto:

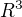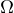Je dána funkce $L$ s definičním oborem $R^{3}$ a kladné číslo $V$ . Mezi všemi oblastmi $\Omega$ splňující podmínky

$[0, 0, 0] \in \Omega , \iiint_{\Omega} \d x \d y \d z=V$

se má nalézt taková, aby integrál $I=\iiint_{\Omega }L{(x,y,z)} \d x \d y \d z$ měl minimální hodnotu.

Připadá mi, že aby taková úloha mohla mít zajímavé řešení, musela by funkce $L$ být poměrně speciální.

Zkus si sám rozmyslet některé jednoduché případy, např. $L{(x,y,z)} = \text{const}$ , $L{(x,y,z)} = x$ a pod.

S nějakou teorií o tom jsem se nesetkal.

check_drummer · 14. 11. 2014 16:04

↑ Brzls:
Ahoj, zajímavé by bylo zkoumat tento problém i v diskrétním případě - pro nějakou trojrozměrnou matici, případně i jednodušeji pro konečnou posloupnost.
Má tento problém jednoduché obecné řešení pokud uvažujeme integrál (a vše okolo) jednorozměrný?

Brzls · 14. 11. 2014 17:22 — Editoval Brzls (15. 11. 2014 14:45)

Mě takováto úloha napadla ve spojitosti s tím, co jste řešili zde http://forum.matweb.cz/viewtopic.php?id=49948 kde je problém ještě složitější o to, že samotná funkce L závisí na oblasti omega. Sice je jasné, že oblast omega musí být celkem dost symetrická ale to tomu stejně moc nepomáhá. Proto mě přirozeně napadlo jestli by nešlo něco podobného řešit pro funkce které záleží pouze na x,y,z.

↑ Rumburak:
Pro L=konst. je to triviální. Pro L=x jsem si myslel že to mám, ale teď mi došlo že jsem uvažoval špatně, to ještě rozmyslim. (edit: minimum neexistuje??)
↑ check_drummer:
Nejsem si jistý. Máme tedy funkci f(x) a hledáme interval délky l, pro který I minimální.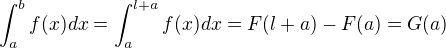

$\int_{a}^{b}f(x)dx=\int_{a}^{l+a}f(x)dx=F(l+a)-F(a)=G(a)$

A hledáme minimum funkce G(a) na množině (-l,l). Pokud bychom připustili možnost, že bod 0 může být krajním bodem toho hledaného intervalu, tak ten interval (-l,l) ve kterém leží a je uzavřený, a na existenci minima by stačila pouze spojitost f(x) (pokud se nepletu čemuž bych se ani nedivil). Jinak bychom se asi museli spokojit pouze s nějakým infimem.

Když nad tím přemýšlím, asi by bylo lepší vypustit požadavek, že ta oblast obsahuje nějaký konkrétní bod, přijde mi že to tam akorát dělá problémy a ani si nejsem jistý proč jsem tam původně takový požadavek chtěl mít.

Brzls · 15. 11. 2014 16:15 — Editoval Brzls (15. 11. 2014 16:19)

Má to třeba smysl zkoušet takto?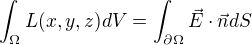

$\int_{\Omega }^{}L(x,y,z)dV=\int_{ \partial \Omega }^{}\vec{E}\cdot \vec{n}dS$
kde vektorová funkce E je řešením rovnice $\nabla \cdot \vec{E}=L$
Otázka - pro které funkce L má tato rovnice řešení?

Předpokládejme, že tedy řešení pro naší funkci existovalo. Pak plochu $\partial\Omega$ vyjádříme parametricky pomocí tří neznámých funkcí $\psi =(\psi _{1}(s,t),\psi _{2}(s,t),\psi _{3}(s,t))$ kde $(s,t)\in \Phi \subset R^{2}$

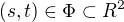
Teď máme tedy nějakou oblast 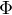$\Phi$ a tři neznámé funkce. Platí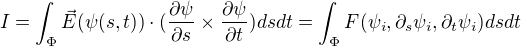

$I=\int_{\Phi }^{}\vec{E}(\psi (s,t))\cdot (\frac{\partial \psi }{\partial s}×\frac{\partial \psi }{\partial t})dsdt=\int_{\Phi }^{}F(\psi _{i},\partial _{s}\psi _{i}, \partial _{t}\psi _{i})dsdt$

Kde funkci F jsme taktéž schopni určit ze zadání

Teď přichází další problematický bod, u kterého netuším na kolik je korektní.
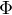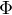Kdybychom předpokládali, že $\Phi$ je pevně daná, tak bychom (možná) byli již schopni určit nějaké podmínky, které by měli neznámé funkce splňovat. Tedy když původní povrch $\partial \Omega$ zobrazujeme na jakoukoli oblast $\Phi$ tak by podle mě mělo pro optimální funkce platit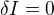

$\delta I=0$

kde delta značí variaci.
To už je ale úloha, jejíž řešení je známé, pro čtyřrozměrný prostor je ve fyzice řešení tohoto problému základem teorie pole.
Řešení pro 4D například zde http://www.physics.purdue.edu/~clarkt/C … ftch21.pdf

Pokud se nepletu, tak ke stejnému tvaru rovnic se dostaneme i v našem dvojrozměrném případě.

Dostaneme tedy soustavu tří parciálních diferenciálních rovnic druhého řádu.
Jenže jak pro ně zformulovat okrajové podmínky? Za jakých předpokladů bude existovat řešení, ke kterým bude existovat 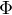$\Phi$ takové, že řešení vážně bude parametrizace pro nějakou uzavřenou plochu (a jak tento požadavek správně formulovat)? Navíc ještě máme podmínku s pevně daným objemem...

Má vůbec smysl to zkoušet řešit tímto způsobem, nebo se ten původní problém akorát ještě více zkomplikoval? Mě intuice říká, že budou existovat původně zadané funkce L, pro které tento postup povede k výsledku, ale nebude jich "moc" a vůbec netuším jak by mohli vypadat resp co splňovat