Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 30. 10. 2014 00:03 — Editoval jelena (14. 11. 2014 14:02)
Zložená funkcia
Cavte ako vyriesim
Nájdite zloženú funkciu  ,
,  , ak funkcia f je definovaná
, ak funkcia f je definovaná
predpisom f(x) = 5 + 4x, 
Jelena: doplněno z jiného tématu (je přehlednější):
Nájdite zloženú funkciu  ,
,  ,ak funkcia f je definovaná predpisom
,ak funkcia f je definovaná predpisom  ,
,  ?
?
Vysledok by mal byt  ,
, 
Offline
- (téma jako vyřešené označil(a) Callme)
#8 14. 11. 2014 14:08 — Editoval Rumburak (18. 11. 2014 10:02)
Re: Zložená funkcia
↑ Callme:
Ahoj.
Kolega ↑ BakyX: Ti odvodil, že každá z funkcí 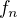 bude tvaru
bude tvaru  , v němž
, v němž
čísla  musí vyhovovat soustavě diferenčních rovnic
musí vyhovovat soustavě diferenčních rovnic
 ,
,

s počátečními podmínkami  ,
,  .
.
Jde tedy o to vyřešit tuto soustavu - třeba metodami, jakými se řeší diferenční rovnice.
Začni tou druhou rovnicí, z níž je patrné, že posloupnost  není závislá na posloupnosti
není závislá na posloupnosti  .
.
Offline
#9 14. 11. 2014 14:26
#10 14. 11. 2014 14:46 — Editoval Rumburak (18. 11. 2014 10:02)
Re: Zložená funkcia
↑ Callme:
O diferenčních rovnicích jsem se zmínil v naději, že jste je probírali. Ale některé jejich případy se dají
vyřešit i bez teorie - "pouhým" úsudkem. Tak je tomu i s rovnici  . Je zřejmé,
. Je zřejmé,
že posloupnost, která je jejím řešením, má pouze kladné členy, takže rovnici můžeme zlogaritomovat (třeba
při základu 4) a tím zjistíme, že  je geometrická posloupnost o kvocientu 2. Zkus pokračovat sám.
je geometrická posloupnost o kvocientu 2. Zkus pokračovat sám.
Offline
#11 14. 11. 2014 15:53 — Editoval Callme (14. 11. 2014 15:57)
Re: Zložená funkcia
↑ Rumburak:
K comu mi je to  ?
?
Vyuzijem nejaky vzorec pre geometricku postupnost?
Offline
#13 15. 11. 2014 21:06
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Zložená funkcia
Zdravím,
a opětuji pozdrav kolegovi ↑ Rumburak: (do tématu). Postupovala jsem tak, že jsem závorky nerozepisovala, tedy např.  , člen obsahující x je vidět i ve Tvé úpravě ↑ Callme:, pokud nebudeš 4 mezi sebou násobit, ale ponecháš jako
, člen obsahující x je vidět i ve Tvé úpravě ↑ Callme:, pokud nebudeš 4 mezi sebou násobit, ale ponecháš jako 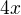 ,
,  ,
,  atd.
atd.
Stejně tak nebudu roznásobovat lineární členy a mám  , po vytknutí
, po vytknutí  , což dává v závorce součet geometrické posloupnosti -prvních n členů, samotnou posloupnost už bys měl vidět.
, což dává v závorce součet geometrické posloupnosti -prvních n členů, samotnou posloupnost už bys měl vidět.
To už bys měl dokončit (pro jistotu překontroluj mé úpravy, zda nemám chybu v počtu n). Bude dobré, pokud potom ještě prokonzultuješ postup, navržený kolegy - bude to pro Tebe mít větší odborný užitek, než to, co píší. Můj návrh se podaří využit? Děkuji.
Offline

 , tak
, tak 
 , kde
, kde 5 a za
5 a za  4x a to je akoze vysledok?
4x a to je akoze vysledok? ,
,  pomocou
pomocou  ,
, 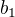 a výsledok bude
a výsledok bude 

 ...
... kde n zacina od 1
kde n zacina od 1



