Matematické Fórum

Callme · 15. 11. 2014 16:33 — Editoval Callme (15. 11. 2014 19:53)

Cavte ako urcim priebeh funkcie
$|\frac{2x^{2}+3}{3x^{2}+5}|$ , $x\in D(f)$
//forum.matweb.cz/upload3/img/2014-11/77603_efeaf.png

Funkcia bude parna, nie je neparna, nie je periodicka D(f)=R, H(f)=R?
Ako urcim nulove body $2x^{2}+3=0$ , $x^{2}=\frac{-3}{2}$ budu komplexne alebo nemozu byt komplexne ?
Body nespojitosti $3x^2+5=0$ , $x^2=\frac{-5}{3}$ rovnako komplexne alebo nemozu byt komplexne ?
Prva derivacia $y'=\frac{4x(3x^2+5)-(2x^2+3)(6x)}{(3x^2+5)^2}=\frac{2x}{(3x^2+5)^2}=\frac{2x}{(3x^2+5)^2}$
Extremy $\frac{2x}{(3x^2+5)^2}=0$ riesenim je $x=0$
Ako urcim intervaly?
Druha derivacia $\frac{2(3x^2+5)^2-2x*2(3x^2+5)*6x}{(3x^2+5)^4}=\frac{2*(3x^2+5)-2x*2*6x}{(3x^2+5)^3}=\frac{-18x^2+10}{(3x^2+5)^3}$
Hodnota funkcie v bode $f(0)=\frac{3}{5}$

jelena · 15. 11. 2014 21:23

Zdravím,

řekla bych, že v komplexním oboru vyšetřovat nemáš, tedy D(f)=R, "nulové body" - rozumím pro odstranění absolutní hodnoty nemáš, jelikož čitatel a jmenovatel jsou jen kladné, proto funkci lze přepsat na $f(x)=\frac{2x^{2}+3}{3x^{2}+5}$ a tak vyšetřovat.

H(f)=R

to už nesouhlasím - může Tvá funkce nabývat záporných hodnot? Pomůže podělit čitatel jmenovatelem pro "lepší viditelnost". Jinak derivace a další kroky v průběhu můžeš také kontrolovat v MAW (pokud bude nějaká nesrovnalost, tak se ozvi), zatím jsem podrobně nekontrolovala, ale vypadá to, že postup derivování a použití derivací ovládáš.

Hodnota funkcie v bode $f(0)=\frac{3}{5}$

to mi vyšlo stejně. Algoritmus kompletního vyšetření máš? Děkuji.

Callme · 15. 11. 2014 21:41

Nulove body v R nebudu?
$H(f)=R^+$ ?
Co je to algoritmus kompletního vyšetření?

jelena · 15. 11. 2014 21:59

Nulove body v R nebudu?

Nulové body pro odstranění absolutní hodnoty nejsou, jelikož čitatel $2x^{2}+3=0$ nemá řešení v R, obdobně jmenovatel $3x^2+5=0$ . Ale víš, že druhá mocnina může být jen nezáporná, tedy součetr nezáporného a kladného čísla je číslo kladné.

Co je to algoritmus kompletního vyšetření?

To je seznam bodů vyšetření + doporučení k jednotlivým krokům - obvykle doporučuji z mathonline (ve studijním textu).

$H(f)=R^+$

to nesouhlasím, poděl, prosím, čitatel jmenovatelem, co vyjde: $\frac{2x^{2}+3}{3x^{2}+5}=\frac{2}{3}+\ldots$ ?

Callme · 15. 11. 2014 22:34 — Editoval Callme (17. 11. 2014 01:09)

↑ jelena:
Vyjde mi $\frac{2}{3}$ a zvysok $-\frac{1}{3}$
Nema ani body nespojitosti v R cize je spojita?
Nie je periodicka takze nema periodu?
Ked je nulovym bodom prvej derivacie 0 tak to znamena ze funkcia ani nerastie ani neklesa a preto nema ani lokalne extremy alebo bude mat intervaly $(-\infty ,0)$ a $(0,\infty )$ ?
Nulovym bodom druhej derivacie je x= $\sqrt{\frac{10}{18}}=\pm \frac{\sqrt{5}}{3}$ cize intervaly budu $(-\infty ,-\frac{\sqrt{5}}{3}) (-\frac{\sqrt{5}}{3},\frac{\sqrt{5}}{3})(\frac{\sqrt{5}}{3},\infty )$ ?
Asymptoty so smernicou $\lim_{x\to\infty }\frac{\frac{2x^{2}+3}{3x^{2}+5}}{x}=\frac{0}{3 }=0$ $\lim_{x\to-\infty }\frac{\frac{2x^{2}+3}{3x^{2}+5}}{x}=\frac{0 }{3 }=0$ alebo sa musi pouzit l'Hospitalovo pravidlo?

jelena · 16. 11. 2014 12:08

↑ Callme:

děkuji, úpravu funkce třeba dopsat do konce $f(x)=\frac{2}{3}-\frac{1}{3(3x^2+5)}$ . Z toho vidíš, že zlomek $\frac{1}{3(3x^2+5)}$ pro x k +oo nebo -oo "odejde do 0", proto obor hodnot funkce bude omezen $\frac{2}{3}$ . Naopak největší hodnotu zlomek $\frac{1}{3(3x^2+5)}$ má pro x=0, ovšem od absolutního členu se odečte, proto kdy $f(0)=\frac{2}{3}-\frac{1}{3(3\cdot 0+5)}$ . To by mělo stačit pro odhad oboru hodnot (a v tomto zadání jde z těchto úvah obor hodnot zapsat i přesně). Jinak bys ho přesně určil přes inverzní funkci, nebo až na závěr celého vyšetření průběhu.

Ked je nulovym bodom prvej derivacie 0 tak to znamena ze funkcia ani nerastie ani neklesa a preto nema ani lokalne extremy alebo bude mat intervaly $(-\infty ,0)$ a $(0,\infty )$ ?

Když 1. derivace je nulová pro x=0, potom je to bod podezřelý z extrému (stacionární bod), vyšetřením změny znaménka 1. derivace bys prokázal, zda je skutečně extrém a typ extrému. Tvůj závěr není dobře - co znamená "mít intervaly"? A jaký je typ extrému v x=0?

U 2. derivace - opět čeho to jsou intervaly? Pro tabulku znamének 2. derivace pravděpodobně.

Asymptoty - ano, podmínka pro l´Hospital je splněna, můžeš používat, dokud půjde, lepší je zapsat po úpravě jako $\lim_{x\to\infty }\frac{2x^{2}+3}{x(3x^{2}+5)}$ .

Jinak pokračuješ dobře, jen se, prosím, drž algoritmu i v komentáři k nalezenému výsledku.

Callme · 16. 11. 2014 12:46

Tie intervaly mam preto aby som zistil ci je rastuca,klesajuca,konvexna,konkavna ci ma lokalne extremy.
Musi sa pouzit l'Hospitalovo pravidlo bez neho vychadzaju obe limity 0?

jelena · 16. 11. 2014 12:52

↑ Callme:

ano, potom to piš, na co jsou intervaly. Jsou to intervaly, na kterých budeš posuzovat znaménko 1. derivace nebo znaménko 2. derivace a dělat závěry, jak jsi napsal.

Musi sa pouzit l'Hospitalovo pravidlo bez neho vychadzaju obe limity 0?

0 vychází i s l´Hospitalem (pokud postupuješ povolenou metodou - vytknutí dominantního členu, porovnáním největších mocnin polynomů, nebo l´Hospital - dokud jde použit, tak bys měl mít stejný výsledek bez ohledu na metodu).

Callme · 17. 11. 2014 00:56 — Editoval Callme (17. 11. 2014 01:14)

Aky bude H(f)= $\frac{2}{3}$ , $\frac{3}{5}$ lebo ja tomu nechapem preco musi ist k 0 a ako si prisla na to ze najväcsiu hodnotu bude mat zlomok pre x=0? Inverzna funkcia bude $y_{1}=\frac{\sqrt{3-5x}}{\sqrt{3x-2}}$ a $y_{2}=-\frac{\sqrt{3-5x}}{\sqrt{3x-2}}$ a z toho urcim ako H(f)?
Na intervale $(-\infty ,0)$ funkcia klesa a na intervale $(0,\infty )$ funkcia rastie cize v 0 je lokalne minimum a 0 je stacionarny bod?
Na intervale je funckia $(-\infty ,-\frac{\sqrt{5}}{3})$ konkavna na intervale $(-\frac{\sqrt{5}}{3},\frac{\sqrt{5}}{3})$ je konvexna a na intervale $(\frac{\sqrt{5}}{3},\infty )$ je konkavna cize $-\frac{\sqrt{5}}{3},\frac{\sqrt{5}}{3}$ su inflexne body?
Asymptota so smernicou bude 0 a bez smernice nebude lebo D(f)=R?
Posledny krok je výpocet limit pro x jdoucí k $\pm \infty$ $\lim_{x\to\infty}\frac{2x^2+3}{3x^2+5}=\frac{2}{3}$ a $\lim_{x\to-\infty}\frac{2x^2+3}{3x^2+5}=\frac{2}{3}$ a to je vsetko?

jelena · 17. 11. 2014 10:15 — Editoval jelena (17. 11. 2014 10:19)

↑ Callme:

ohledně oboru hodnot - upravili jsme funkci do takového předpisu $f(x)=\frac{2}{3}-\frac{1}{3(3x^2+5)}$ , kde vidíme, jakých hodnot může funkce nabývat, jen si takový rozbor udělej pouhým pohledem na předpis - x je definováno na celém R, jmenovatel zlomku je kvadratická funkce $h(x)=3(3x^2+5)$ , která má minimum v x=0, naopak tomu bude odpovídat maximální hodnota zlomku atd. ohledně chování v +/- nekonečnu. Jen si to tak pomalu probírej.

Jiný způsob - (více univerzální) přes inverzní: máš $f^{-1}(x)_1=\sqrt{\frac{3-5x}{3x-2}}$ def. obor je $\frac{3-5x}{3x-2}\geq 0$ (def. obor inverzní bude odpovídat oboru hodnot původní funkce). Správně máš 2 větvě inverzních funkcí - původní funkce nebyla prostá.

Pro obor hodnot by mělo vycházet $\langle f(0)\,,\frac{2}{3})$ (levou hranici přepočti, prosím).

Na intervale $(-\infty ,0)$ funkcia klesa a na intervale $(0,\infty )$ funkcia rastie cize v 0 je lokalne minimum a 0 je stacionarny bod?
Na intervale je funckia $(-\infty ,-\frac{\sqrt{5}}{3})$ konkavna na intervale $(-\frac{\sqrt{5}}{3},\frac{\sqrt{5}}{3})$ je konvexna a na intervale $(\frac{\sqrt{5}}{3},\infty )$ je konkavna cize $-\frac{\sqrt{5}}{3},\frac{\sqrt{5}}{3}$ su inflexne body?

to se mi zdá v pořádku, ale překontroluj si to, prosím v MAW.

Asymptota so smernicou bude 0 a bez smernice nebude lebo D(f)=R?

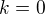Bez směrnice souhlasím. Asymptotu se směrnici jsi nekončil, počítal jsi $y=kx+q$ , našel jsi $k=0$ (výpočet s l´Hospital, ale nedokončil $q$ .

Poslední krok v pořádku, výsledek by Tobě měl souhlasit i s výsledkem asymptot z předchozího kroku - tedy opravu předchozí krok ještě.

Podle Tvého papíru ještě máš mít tabulku znamének funkce, ale to jsme již prodiskutovali, že všude kladná. Chybí něco nebo něco není jasné? Děkuji.

Callme · 17. 11. 2014 17:21 — Editoval Callme (17. 11. 2014 18:13)

D(f) inverznej pre $\sqrt{\frac{3-5x}{3x-2}}$ je $3-5x\ge =0\Rightarrow x\le \frac{3}{5}$ a $3x-2> 0\Rightarrow x>\frac{2}{3}$ cize H(f) povodnej $\frac{2}{3}<x\le \frac{3}{5}$ co je nezmysel.
q= $\lim_{x\to\pm \infty }(f(x)-kx)=\lim_{x\to\pm \infty }(\frac{2x^2+3}{3x^2+5}-0*x)=\lim_{x\to\pm \infty }\frac{2x^2+3}{3x^2+5}=\frac{2}{3}$ cize asymptota so smernicou bude $\frac{2}{3}$ .

jelena napsal(a):
Podle Tvého papíru ještě máš mít tabulku znamének funkce, ale to jsme již prodiskutovali, že všude kladná.

Kladnost a zapornost sa urcuje podla coho z povodnej funkcie kde vidim ze funkcia je kladna na intervale 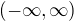$(-\infty ,\infty )$ ? Pri $f'(x)$ a $f''(x)$ ako urcim intervaly na ktorych je $f$ definovana?

Callme napsal(a):
Na intervale $(-\infty ,0)$ funkcia klesa a na intervale $(0,\infty )$ funkcia rastie cize v 0 je lokalne minimum a 0 je stacionarny bod?
Na intervale je funkcia $(-\infty ,-\frac{\sqrt{5}}{3})$ konkavna na intervale $(-\frac{\sqrt{5}}{3},\frac{\sqrt{5}}{3})$ je konvexna a na intervale $(\frac{\sqrt{5}}{3},\infty )$ je konkavna cize $-\frac{\sqrt{5}}{3},\frac{\sqrt{5}}{3}$ su inflexne body?

Intervaly nemaju obsahovat zlozene zatvorky?

jelena · 17. 11. 2014 19:08

co je nezmysel.

Řešil jsi nerovnici $\frac{3-5x}{3x-2}\geq 0$ , tak to ještě překontroluj řešení - WA dává výsledek tak, lepší je přepsat na $\frac{5x-3}{3x-2}\leq 0$ .

Asymptota se směrnici souhlasí. Kladnost a zápornost pro původní funkci - ano, je kladná na celém def. oboru, na R.

Def. obory derivací - jelikož derivováním vytvoříš nové předpisy funkcí, tak u nich také posuzuješ def. obory (říkáme, že hledáme i kde derivace neexistuje), ale def. obory derivací u Tebe jsou stejné, jako původní funkce, derivováním nepřibylo žádné nové omezení do podmínek.

Intervaly nemaju obsahovat zlozene zatvorky?

podle mne ne. Případně přidej, prosím, nějaký vzor zápisu intervalů, kde byly i složené závorky. Děkuji.

Callme · 17. 11. 2014 20:07 — Editoval Callme (17. 11. 2014 20:22)

Mne vychadza vyriesenim nerovnice $\frac{2}{3}<x\le \frac{3}{5}$ na WA vychadza $\frac{2}{3}>x\ge \frac{3}{5}$ a chybu nevidim. Kedze neexistuju v R body nespojitosti to znamena ze funkcia nemoze byt nespojita a bude potom spojita a u nej urcim intervaly ako?
Funkcia nema body nespojitosti cize nebude mat ani limitu v bodoch nespojitosti.

Callme napsal(a):
Posledny krok je výpocet limit pro x jdoucí k $\pm \infty$ $\lim_{x\to\infty}\frac{2x^2+3}{3x^2+5}=\frac{2}{3}$ a $\lim_{x\to-\infty}\frac{2x^2+3}{3x^2+5}=\frac{2}{3}$ a to je vsetko?

Touto limitou sa mysli limita v dolezitych bodoch ktoru ju nutne rovnako urcit podla zoznamu v #1?

jelena · 17. 11. 2014 20:32

↑ Callme:

řešení nerovnice - pořádně překontroluj tabulku nulových bodů a znamének pro $\frac{5x-3}{3x-2}\leq 0$ (kontrola - zlomek je záporný, pokud čitatel a jmenovatel mají různá znaménka). Nemáš třeba chybu, jak jsi umístil na číselnou osu? $\frac{3}{5}$ je menší, než $\frac{2}{3}$ , někde chyba bude (viz i Tvůj graf funkce už bys ho měl mít).

Kedze neexistuju v R body nespojitosti to znamena ze funkcia nemoze byt nespojita a bude potom spojita a u nej urcim intervaly ako?
Funkcia nema body nespojitosti cize nebude mat ani limitu v bodoch nespojitosti.

K tomuto jen napíšeš cca ve smyslu "Funkce nemá body nespojitosti, proto nevyšetřujeme limity v takových bodech a funkce je definována na celém R".

Touto limitou sa mysli limita v dolezitych bodoch ktoru ju nutne rovnako urcit podla zoznamu v #1?

ano, zde bych rozuměla v bodech nespojitosti a na koncích definičního oboru - body nespojitosti nemáme, nevyšetřujeme. Na koncích def. oboru - pro +oo a -oo jsi vyšetřil.

Ať se podaří dokončit, nebudu už online, více nezkontroluji cca až do zítra večera (ale to už věřím, že dokončíš).

Callme · 18. 11. 2014 00:22

Graf funkcie ma vyzerat rovnako ako na MAW? Dakujem.

jelena · 18. 11. 2014 10:10

↑ Callme:

ano, mělo by to vycházet stejně (taková "křídla" mi vycházejí s minimem pro x=0), musíš ale trošku "ošidit měřítko" - obor hodnot je hodně úzký, tak aby vůbec něco bylo vidět.

Callme · 18. 11. 2014 11:06

Je nutne zakreslit aj asymptotu ako na MAW? Posledne co by som potreboval zistit ako je to s tou spojitostou funkcia bude spojita alebo nespojita alebo nic z toho?

Jj · 18. 11. 2014 11:37 — Editoval Jj (18. 11. 2014 11:37)

↑ Callme:

Dobrý den.

Vyšetřovaná funkce je spojitá. Asymptotu určitě uvést a zakreslit.

Matematické Fórum

#1 15. 11. 2014 16:33 — Editoval Callme (15. 11. 2014 19:53)

Priebeh funkcie

#2 15. 11. 2014 21:23

Re: Priebeh funkcie

#3 15. 11. 2014 21:41

Re: Priebeh funkcie

#4 15. 11. 2014 21:59

Re: Priebeh funkcie

#5 15. 11. 2014 22:34 — Editoval Callme (17. 11. 2014 01:09)

Re: Priebeh funkcie

#6 16. 11. 2014 12:08

Re: Priebeh funkcie

#7 16. 11. 2014 12:46

Re: Priebeh funkcie

#8 16. 11. 2014 12:52

Re: Priebeh funkcie

#9 17. 11. 2014 00:56 — Editoval Callme (17. 11. 2014 01:14)

Re: Priebeh funkcie

#10 17. 11. 2014 10:15 — Editoval jelena (17. 11. 2014 10:19)

Re: Priebeh funkcie

#11 17. 11. 2014 17:21 — Editoval Callme (17. 11. 2014 18:13)

Re: Priebeh funkcie

jelena napsal(a):

Callme napsal(a):

#12 17. 11. 2014 19:08

Re: Priebeh funkcie

#13 17. 11. 2014 20:07 — Editoval Callme (17. 11. 2014 20:22)

Re: Priebeh funkcie

Callme napsal(a):

#14 17. 11. 2014 20:32

Re: Priebeh funkcie

#15 18. 11. 2014 00:22

Re: Priebeh funkcie

#16 18. 11. 2014 10:10

Re: Priebeh funkcie

#17 18. 11. 2014 11:06

Re: Priebeh funkcie

#18 18. 11. 2014 11:37 — Editoval Jj (18. 11. 2014 11:37)

Re: Priebeh funkcie

Zápatí