Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 17. 11. 2014 13:39
- terezkaaaaa5

- Příspěvky: 1221
- Reputace: 2
Limity posloupností
Dobrý den, poradíte mi prosím s těmito příklady?
1) 
2) 
Obě limity platí pro n jdoucí k nekonečnu.
Bohužel si s tím nevím rady. Předem děkuji za pomoc.
Offline
- (téma jako vyřešené označil(a) terezkaaaaa5)
#3 17. 11. 2014 15:28
- terezkaaaaa5

- Příspěvky: 1221
- Reputace: 2
Re: Limity posloupností
↑ bonifax:
Potom to bude:
Je to tak? :)
Offline
#4 17. 11. 2014 15:35
#5 17. 11. 2014 15:38
- terezkaaaaa5

- Příspěvky: 1221
- Reputace: 2
Re: Limity posloupností
↑ bonifax:
Děkuji. A ten druhý prosím? Jak je to zadané takto obecně, tak si vůbec nevím rady.
Offline
#6 17. 11. 2014 15:46
#7 17. 11. 2014 15:49 Příspěvek uživatele Kdosi byl skryt uživatelem Kdosi. Důvod: Už zbytečné
#8 17. 11. 2014 15:52
- terezkaaaaa5

- Příspěvky: 1221
- Reputace: 2
Re: Limity posloupností
↑ bonifax:
Děkuji, ale bohužel mi to nepomohlo. Stejně nevím co s tím.
Offline
#9 17. 11. 2014 16:09 — Editoval bonifax (17. 11. 2014 16:11)
Re: Limity posloupností
↑ terezkaaaaa5:
V čitateli je nějaký součet aritimetické posloupnosti pro kterou platí, že: - první člen je 1
- první člen je 1 - n-tý člen je 2n-1
- n-tý člen je 2n-1
Vzorec pro součet AP je, použij ho v čitateli: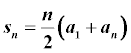
Tedy takto:
Offline
#10 17. 11. 2014 16:12
- terezkaaaaa5

- Příspěvky: 1221
- Reputace: 2
Re: Limity posloupností
↑ bonifax:
Mockrát děkuji. Měli by to tedy vyjít + nekonečno, že? :)
Offline
#11 17. 11. 2014 16:14 — Editoval terezkaaaaa5 (17. 11. 2014 16:16)
- terezkaaaaa5

- Příspěvky: 1221
- Reputace: 2
Re: Limity posloupností
A měla bych prosím ještě jeden příklad: 
Výraz jsem si upravila jako:  , ale nevím, zda je to "legální" úprava.
, ale nevím, zda je to "legální" úprava.
Offline
#13 17. 11. 2014 17:44
- terezkaaaaa5

- Příspěvky: 1221
- Reputace: 2
Re: Limity posloupností
↑ bonifax:
To je na mě nějaké těžké. Pokud vytknu  , tak mi vyjde:
, tak mi vyjde: 
Offline
#14 17. 11. 2014 21:35 — Editoval bonifax (17. 11. 2014 21:53)
Re: Limity posloupností
↑ terezkaaaaa5:
Myslel jsem jen pod tou odmocninou, takhle)
Po chvíli počítání tímto postupem (1) vyjde neurčitý výraz. Znamená to, že je třeba na to jít jinak. Nevadí, napodruhé zkusíme rozšiřování (2).
To už zdá se být na dobré cestě. Po dlouhém výpočtu, vyjde výsledek  .
.
(1)![kopírovat do textarea $lim (\sqrt{n^{2}+n}-n)= lim(\sqrt{n^2(1+\frac{1}{n}})-n=lim\sqrt{n^2}(\sqrt{1+\frac{1}{n}}-1)=lim (n(\sqrt{1+\frac{1}{n}}-1))=[0*\infty ]=NaN$](/mathtex/cf/cf5f9582266584ab76b8170ff7db5914.gif)
(2)

Offline

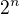 , exponencionálu o nejvyšším základu.
, exponencionálu o nejvyšším základu. z celýho výrazu.
z celýho výrazu.