Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 22. 11. 2014 18:06
Limita funkce s x v mocnině
Ahoj, omlouvám se, jestli se ptám na úplnou kravinu, kterou lze spočítat jednoduše. Po celodenním učení jsem už ale trochu zmatený a s tímhle příkladem si nevím moc rady :) Potřebuji spočítat jednu část příkladu - ten obsahuje limitu, u které se x blíží k nekonečnu a jako funkce je zde výraz se stejnou mocninou a různými základy (viz níže). Jak by se taková limita počítala? Připadá mi logické, že podle toho, zda je a nebo b větší je jasné, zda bude výsledek kladné nebo záporné nekonečno. Myslím ale, že stejně by u takového příkladu měl být nějaký postup a ten mně není jasný. 
Platí tedy že když:
a
?
Předem díky za odpověď
Offline
#2 22. 11. 2014 20:15
Re: Limita funkce s x v mocnině
Zkus tam přidat nějaké podmínky a trochu si s tím pohrát.
Proč se ptáš jestli platí něco. Proč si to nevyzkoušíš na nějakých příkladech?
Pro mě (a zřejmě i pro mnoho ostatních) je
ale nepřijde mi, že by
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#3 22. 11. 2014 20:25
Re: Limita funkce s x v mocnině
Díky za odpověď, ale potřeboval bych něco konkrétnějšího. Dejme tomu, že místo a a b bude 3 a 4. Jak bych si tohle odůvodnil u písemky? Když napíšu že
a proto je limita rovna mínus nekonečno, pochybuji, že mi to uznají.
Jinak samozřejmě to s 1 a 0 je pravda. Jde mi spíš o ten správný postup. To, že je "jedno nekonečno větší než druhé" mi nikdy neuznali, vždy bylo potřeba něco vytknout, či rozšířit zlomek apod., aby to bylo jasnější.
Offline
#4 22. 11. 2014 21:17 — Editoval Freedy (22. 11. 2014 21:17)
Re: Limita funkce s x v mocnině
Ahoj,
je nutné tento problém rozkouskovat na vícero částí.
Začneme s tou nejjednodušší:
1) za tohoto předpokladu lze tvrdit že
za tohoto předpokladu lze tvrdit že
Proč? Vytknutím dominantního členu (v tomto případě a^x) dostáváme:
2) úplně obdobný postup, jen na konci vyjde -nekonečno.
úplně obdobný postup, jen na konci vyjde -nekonečno.
3) 

4)  obdobný postup, jen s tím že vyjde +nekonečno.
obdobný postup, jen s tím že vyjde +nekonečno.
5) 

6) 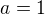
a)  >>>
>>> 
b)  >>>
>>> 
7) 
a)  >>>
>>>
b) 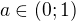 >>>
>>> 
8) 

9) 

10) 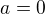
a)  >>>
>>>
b)  >>>
>>> 
11) b = 0
a)  >>>
>>> 
b) 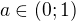 >>>
>>> 
pro záporná čísla stejná teorie. Pouze s tím že když bude a nebo b menší než -1 nebude daná limita existovat.
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#6 22. 11. 2014 21:33 — Editoval jarrro (22. 11. 2014 21:34)
Re: Limita funkce s x v mocnině
keďže je tam x tak predpokladám, že ide o limitu funkcie teda záporné a, b sa neuvažujú potom je potrebné to rozdeliť na pár prípadov
edit: hups som to trochu dlho písal nechám to už tu
MATH IS THE BEST!!!
Offline
