Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Maclaurinov polynóm (TOTO TÉMA JE VYŘEŠENÉ)
#4 26. 11. 2014 14:19
Re: Maclaurinov polynóm
Ahoj,
Je uzitocne poznat vety na tuto temu.
Lopatisticka odpoved...( pozri teoriu: Mc polynom a zlozene funkcie)
V tvojom pripade mozes vyuzit Mc polynom ° 12, pre cos x, a potom hladany polynom  dostanes ze nahradis x, v Mc pol. pre cos x z clenom
dostanes ze nahradis x, v Mc pol. pre cos x z clenom 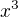 ale tak ze pri vypocte ignorujes vsetky x co maju vyssiu mocninu ako 12.
ale tak ze pri vypocte ignorujes vsetky x co maju vyssiu mocninu ako 12.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#6 26. 11. 2014 15:58
Re: Maclaurinov polynóm
↑ Callme:
V tvojom cvicenie sa hovori len o polynôme, zvysok od teba, v tomto cviceni, nie je ziadany.
(Ak chces dokazat takyto vysledok, to najdes v bezny y knihach, a iste aj v tvojich materialoch).
Napis pre kontrolu tvoje riesenie tohto cvicenia.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#8 27. 11. 2014 09:36
Re: Maclaurinov polynóm
↑ Callme:
Výsledek  je dobře, ale cestu k němu je potřeba mírně poopravit
je dobře, ale cestu k němu je potřeba mírně poopravit
po formální stránce.
Není možno zde psát  - to by byla rovnice s neznámou
- to by byla rovnice s neznámou  . Pro hodnoty funkce
. Pro hodnoty funkce 
je potřeba zavést novou proměnnou, např.
(1) 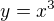 .
.
Nyní vezměme ML polynom dostatečně vysokého stupně k funkci  , třeba
, třeba
 .
.
Sem dosadíme z (1)a máme
 ,
,
což je ML polynom funkce  st. 18. Nás zajímá ML polynom st. 12, tedy
st. 18. Nás zajímá ML polynom st. 12, tedy
 .
.
Třeba tak.
Offline
#9 27. 11. 2014 10:22 — Editoval vanok (27. 11. 2014 10:29)
Re: Maclaurinov polynóm
CPozdravujem ↑ Rumburak:,↑ Callme:
Prave som cital posledne prispevky, a prispevok kolegu ↑ Rumburak: je prakticky co by com poznamenal.
Asi ide o preklep v ↑ Callme:, kde si myslim ze podla tvojho uvodneho prispevku si chcel napisat : na prvom riadku 
Tiez na druhom si iste chcel pisat vsetko z s, miesto x, co konecne da hladany vysledok ktory si napisal na poslednom riadku.
To vsetko vdaka teorii limitovanych rozvojov zlozenych funkcii... Ktoru naznacil aj kolega ↑ Rumburak: v poslednej casti jeho prispevku.
Vo sk a cz nepoznam ziadny text na tu temu. Napr v fr ( ako aj egl.) je plno takych praktickych textov ( na urovni prveho rocnika univerzity). Nahodne klik na Google da http://www.math.univ-toulouse.fr/~mlutz … imites.pdf co ti moze pomoct napisat dokaz pouzitej vety, ak by si to raz potreboval.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Maclaurinov polynóm (TOTO TÉMA JE VYŘEŠENÉ)
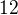 pre funkciu
pre funkciu  .
. co zaberie par stran?
co zaberie par stran? cize
cize  ?
? , kde
, kde  , je řada
, je řada 
 , potom jde o MacLaurinovu řadu funkce
, potom jde o MacLaurinovu řadu funkce  .
.  .
. ?
?
 funkciu
funkciu  tak tym nevyuzivam substituciu a to co bude mat mocninu väcsiu ako 12 tak bude zvyskom?
tak tym nevyuzivam substituciu a to co bude mat mocninu väcsiu ako 12 tak bude zvyskom?
 bude taky polynom
bude taky polynom