Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 27. 11. 2014 16:44
Re: derivace a definiční obory
↑ Janca96:V ulohach  ide o vztahy pre derivaciu suctu, sucinu a podielu funkcii. Pozri si ich a skus na tieto funkcie pouzit. Ak vznikne problem, ozvi sa. Potom sa pozrieme na ostatne.
ide o vztahy pre derivaciu suctu, sucinu a podielu funkcii. Pozri si ich a skus na tieto funkcie pouzit. Ak vznikne problem, ozvi sa. Potom sa pozrieme na ostatne.
Offline
#3 27. 11. 2014 18:00 — Editoval Janca96 (27. 11. 2014 19:53)
Re: derivace a definiční obory
↑ vlado_bb: v příkladech g1, g2, g4, g5, g7, g8 a g9 už jsem se dopracovala k výsledku (snad správnému :))
g3 mám zatím takto a nevím jestli to jde nějak zjednodušit: 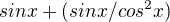
s ostatními příklady si už nevím rady
ještě bych potřebovala poradit s definičními obory
Offline
#4 27. 11. 2014 18:48 Příspěvek uživatele tomas janeta byl skryt uživatelem tomas janeta. Důvod: Pomýlil som sa
#5 27. 11. 2014 20:15
- tomas janeta
- Příspěvky: 67
- Škola: gymnázium antona bernoláka námestovo
- Pozice: študent
- Reputace: 5
Re: derivace a definiční obory
Vždy skús použiť deriváciu súčtu ,súčinu a zloženej funkcie (najprv si ich môžeš nejako upraviť napr.
Potom dg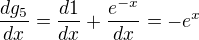
Ak ide o definičné obory 1.v menovateli nesmie byť nula
2.pod odmocninou nesmie byť záporné číslo
Príklad:![kopírovat do textarea $g_{6}(x)=\frac{x^{2}\sqrt[3]{x}}{\sqrt{x}}=x^{2+1/3-1/2}$](/mathtex/96/969274dda1c0b68c88cedbc6d3eaf288.gif)
Teda ![kopírovat do textarea $g_{6}(x)=x^{1+5/6}=x*\sqrt[6]{x^{5}}$](/mathtex/78/7815eb3ed2c208462081883617e8f135.gif)
Takže 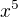 nesmie byť záporné číslo ono je záporné vtedy a len vtedy ak je záporné x (ak uvažujeme len reálne čísla)
nesmie byť záporné číslo ono je záporné vtedy a len vtedy ak je záporné x (ak uvažujeme len reálne čísla)
P.S.:som prvák na strednej ,a tak sa môžem mýliť
Offline
#6 27. 11. 2014 20:20
- tomas janeta
- Příspěvky: 67
- Škola: gymnázium antona bernoláka námestovo
- Pozice: študent
- Reputace: 5
Re: derivace a definiční obory
Ešte jedno P.S.: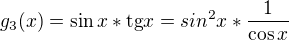
(derivácia súčinu a zloženej funkcie)
Offline
#7 27. 11. 2014 20:40
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: derivace a definiční obory
Zdravím,
jen laskavá moderátorská - v tématu má být jen jedna úloha (není námitka mít tematický okruh, pokud se např. hledá vhodný studijní materiál nebo doporučení obecného postupu). Tedy zde dodiskutujte derivace, na def. obory - prosím nové téma a po jedné úloze ↑ Janca96:. viz pravidla.
Děkuji.
To bude lepší bez úpravy - jako derivace součinu. 
Ešte jedno P.S.
:-) pro některá P.S. lepší samostatná témata (pro každou derivaci také). Děkuji.
Offline
#8 27. 11. 2014 21:16
Re: derivace a definiční obory
↑ Janca96:K dotycniciam: dotycnica je priamka, teda jej predpis je  . Ak ide o dotycnicu k funkcii
. Ak ide o dotycnicu k funkcii  v bode
v bode  a existuje vlastna (teda realna) derivacia v tomto bode, tak
a existuje vlastna (teda realna) derivacia v tomto bode, tak 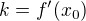 . No a
. No a  dopocitas z toho, ze poznas jeden bod dotycnice, konkretne bod
dopocitas z toho, ze poznas jeden bod dotycnice, konkretne bod ![kopírovat do textarea $[x_0,f(x_0)]$](/mathtex/a7/a76efd101c8b55aaabb4d8ae551d8356.gif) .
.
Offline
#9 27. 11. 2014 21:25
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: derivace a definiční obory
↑ vlado_bb:
Zdravím,
máš pravdu, tečny jsem nepostřehla :-) Tečny, prosím, diskutujte v samostatném tématu. Děkuji.
Offline


