Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Mal'cev, Malcev, Maltsev product, součin (TOTO TÉMA JE VYŘEŠENÉ)
#1 20. 11. 2014 12:41
Mal'cev, Malcev, Maltsev product, součin
Dobrý den,
OT: po půlhodině hledání texovského "m" v kroužku to vzdávám, budu psát (m), pokud to někdo umíte napsat sem do fóra, prosím.
Na netu moc materiálu o (m) součinu není a tak uvedu dvě pdf, tedy hledá se odborník na (m) :)
[1] http://www.liafa.jussieu.fr/~jep/PDF/Malcev.pdf
[2] http://cmup.fc.up.pt/cmup/jalmeida/prep … bility.pdf
přičemž postupuji podle definice toho druhého textu "On the irreducibility of pseudovarieties..."







Pseudovarieta V je Mal'cev idempotent, pokud V(m)V=V
Následující pseudovariety jsou "zřejmě" (m) idempotentní:
(takovou tu fajn závorku jako v [2] taky neumim)








K tomu bych se ještě dostal, ale více mě zajímá asociativita.
Prý platí jen jedna inkluze:
(odborník na tex nejsem, prosím, omluvte případné hnusy)
Nyní bych rád rozluštil, co tato inkluze říká. Pokud na to budu nakonec sám, tak se to tady pokusím postupně rozkrývat.
Buď S konečná pologrupa, která patří do levé strany:
Chceme pak ukázat, že bude platit aji:








Díky,
kolejo
Offline
- (téma jako vyřešené označil(a) kolejo)
#2 24. 11. 2014 10:58
Re: Mal'cev, Malcev, Maltsev product, součin
Rozepisoval jsem si to znovu (asociativitu) a opravdu nevím, jak to do toho vložit a proč nebude platit ta druhá implikace.
Tak aspoň krátké zamyšlení nad (m) idempotentem Sl (polosvazy)
Sl (m) Sl = Sl
jedna inkluze jasná
z té druhé... nechť S patří do Sl(m)Sl
Pak máme phi: S -> T homomorfismus, T polosvaz, takže vzory všech prvků polosvazu T (protože všechny jsou idempotentní) v homomorfimus phi jsou polosvazy.
Je S polosvaz? To nás teď přece zajímá.
Vezměme za T polosvaz {1,0}. Polosvaz, který je vzorem jedničky označím A, pro nulu to bude B.
Pologrupa S pak bude sjednocení A a B, kde A je nad B a a*b patří do B, b*a taky. b1*b2 v B, a1*a2 jasně v A. Pak S je polosvaz a tedy patří do Sl, tedy Sl je skutečně (m)-idempotent
Je tato úvaha správná?
Je fajn si s tím lámat hlavu, za pár dní už v tom bude snad jasno.
Offline
#3 28. 11. 2014 00:45 — Editoval OiBobik (29. 11. 2014 23:09)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Mal'cev, Malcev, Maltsev product, součin
↑ kolejo:
Ahoj,
zkusím tu inkluzi, co má platit.
0) předpokládám, že pseudovarieta generovaná množinou/třídou  je
je  , je to tak?
, je to tak?
1) Ověřme inkluzi na generátorech variety. Tj. vezměme generátor variety  . Tedy máme
. Tedy máme 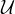 -homomorfismus
-homomorfismus  , kde
, kde  .
.
Co to znamená, že  : to je, že
: to je, že  , kde
, kde  je generující množina
je generující množina  z definice.
z definice.
Tedy: existují  a kongruence
a kongruence  na
na  , že
, že  a
a  jsou generátory
jsou generátory  z definice.
z definice.
Tedy existují  -homomorfismy
-homomorfismy  s
s  .
.
2) To je trochu komplikované, tak se to pokusme zredukovat. Nejprve zkusíme zapomenout na produkt, tj nahlédnout, že pokud byly 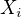 generátory
generátory  z definice, pak i jejich součin je takovým generátorem.
z definice, pak i jejich součin je takovým generátorem.
Jinými slovy, uvažme 
tj. zobrazení definované předpisem  . To je zřejmě stále homomorfismus. Chceme však, že je to
. To je zřejmě stále homomorfismus. Chceme však, že je to  -homomorfismus. Předně
-homomorfismus. Předně  , jelikož
, jelikož  je uzavřeno na konečné součiny. Nechť dále
je uzavřeno na konečné součiny. Nechť dále  je idempotent, což je ekvivalentní tomu, že každý
je idempotent, což je ekvivalentní tomu, že každý 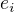 je idempotent ve
je idempotent ve  . Pak máme, že
. Pak máme, že  pro každé
pro každé  . Pak ovšem
. Pak ovšem 
z uzavřenosti  na konečné produkty.
na konečné produkty.
Tedy místo součinu lze búno brát pouze jeden generátor, tj máme  ,
,  ,
, 
 -homomorfismus s
-homomorfismus s  .
.
Teď se zbavíme té inkluze  . To je celkem přímočaré: Máme
. To je celkem přímočaré: Máme  . Přitom, je-li
. Přitom, je-li  idempotent, je
idempotent, je  a pak je
a pak je  , jelikož
, jelikož  je uzavřená na podalgebry.
je uzavřená na podalgebry.
Celkem tedy lze búno předpokládat, že  , kde máme
, kde máme 
 -homomorfismus s
-homomorfismus s  .
.
3) To už je docela dobrý: Máme
kde ![kopírovat do textarea $\pi: x \mapsto [x]_{\sim}$](/mathtex/62/628f179e289aabfe8d706acfe453b371.gif) je projekce.
je projekce.
Teď je trik, který nevím, jak bych obcházel: Vezmeme pullback  a
a  , tj
, tj
spolu se zobrazeními
Snadno si přitom člověk rozmyslí, že  je opět pologrupa (nebo o čemže se to bavíme) a
je opět pologrupa (nebo o čemže se to bavíme) a  jsou homomorfismy. Taky si všimni, že
jsou homomorfismy. Taky si všimni, že  je surjektivní, jelikož
je surjektivní, jelikož  je surjektivní.
je surjektivní.
Teď máme príma složeninu
a chceme teď o ní tvrdit, že je to  -homomorfismus. Tj. fixujme idempotent
-homomorfismus. Tj. fixujme idempotent  . Pak
. Pak  , to už víme. Teď chceme ukázat, že
, to už víme. Teď chceme ukázat, že  , jinými slovy, ideálně hledáme
, jinými slovy, ideálně hledáme 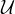 -homomorfismus
-homomorfismus  . Kandidát, co máme na
. Kandidát, co máme na  je asi jasný, a sice
je asi jasný, a sice  (co jinýho bychom vymysleli, že).
(co jinýho bychom vymysleli, že).
Přitom
a jako vhodné zobrazení se nabízí opět projekce  .
.
Pak je-li  idempotent, je nutně i
idempotent, je nutně i ![kopírovat do textarea $[x]_{\sim}$](/mathtex/4b/4bdaeccacaa30a4b983339e2d2b16cde.gif) idempotent. Tedy (teď používáme, že
idempotent. Tedy (teď používáme, že  je
je 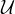 -homomomorfismus)
-homomomorfismus) ![kopírovat do textarea $\varphi^{-1}([x]_{\sim}) \in \mathcal{U}$](/mathtex/72/72daa1f6045a1102a3561e9311bf2cc3.gif) .
.
Pak ovšem ![kopírovat do textarea $(\varphi')^{-1}(x)=\varphi^{-1}([x]_{\sim})\times\{x\} \simeq \varphi^{-1}([x]_{\sim}) \in \mathcal{U}$](/mathtex/d3/d3a7ccb72cbf7ba7868071623ecce0f8.gif) . To jsme chtěli.
. To jsme chtěli.
4) Kde tedy teď jsme, je, že máme  . Zbývá už jen tam dostat
. Zbývá už jen tam dostat  . Ovšem vzpomeň si, že
. Ovšem vzpomeň si, že  bylo surjektivní - tedy,
bylo surjektivní - tedy,  je nějaký faktor
je nějaký faktor  , tedy opět v
, tedy opět v  .
.
Uf.
Docela makačka. To máš k bakalářce nebo něčemu takovému?
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#4 28. 11. 2014 11:53
Re: Mal'cev, Malcev, Maltsev product, součin
↑ OiBobik:
Dobrý den,
děkuju moc, ještě jsem to celý nečetl, jen jsem to proletěl, dostanu se k tomu asi až o víkendu.
Děkuju zvlášť za "emko" v kolečku.
OT: zkusím to taky 
Ano, tohle je část mé bakalářky. Hlavním tématem je takový jiný součin a mám se podívat, jestli nějak souvisí se "známými" součiny, tak se tedy seznamuji s Mal'cevem.
Almeida píše o spoustě věcech, jak je to jasný a zřejmý. No.
Ještě se na to podívám,
pěkný víkend přeju
Offline
#5 28. 11. 2014 12:18 — Editoval OiBobik (28. 11. 2014 13:34)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Mal'cev, Malcev, Maltsev product, součin
↑ kolejo:
Vpoho, já typicky tak dlouhé příspěvky zpravidla ani nečtu, takže zcela chápu. Ale když to člověk přece jen tak nějak projde, tak si uvědomí několik zakopaných psů, zejména
1) Ten součin je definovaný pomocí nějakých generátorů, takže samotná pseudovarieta je pak  , kde
, kde  je ta množina generátorů z definice. Takže pak už člověku nepřijde až tak divné, že projde "jen" jedna inkluze, ale spíš je mu divné, že projde vůbec nějaká inkluze.
je ta množina generátorů z definice. Takže pak už člověku nepřijde až tak divné, že projde "jen" jedna inkluze, ale spíš je mu divné, že projde vůbec nějaká inkluze.
(Viz tam ty redukce "faktor podalgebry produktu generátorů -> faktor podalgebry generátoru ->faktor generátoru", kde toho "faktor" se už člověk nezbaví a musí to obejít tím pullbackem. EDIT: možná by bylo konceptuálně lepší vzít místo daného pullbacku raději pushout z  a dostat tak něco, co je v opět tím příslušným typem generátoru... nevím, jestli to bude fungovat, ale zdá se mi, že jo)
a dostat tak něco, co je v opět tím příslušným typem generátoru... nevím, jestli to bude fungovat, ale zdá se mi, že jo)
2) Je tam asi několikrát implicitně formulováno, co to ta inkluze vlastně říká (a je vidět, že to není žádný příliš kompaktní výrok) a vlastně mi přijde, že aby tomu člověk tak nějak rozuměl, tak nějakou takovou eskapádu udělat více či méně musí (opět asi největší zrada je v tom  -uzávěru).
-uzávěru).
(Možná by k tomu šla přifařit nějaká pseudogeometrická intuice, ale bylo mi řečeno, že moje náhledy v univerzále jsou špatně, tak to radši zmiňovat nebudu.)
a OT:
Docela dobrý algoritmus na hledání, jak se co TeXá, je
1) googlit "Latex displaying a formula" a na wiki je celkem vyčerpávající list standardních matematických symbolů v TeXu, a když to selže, tak
2) googlit "Latex <what I want to be able to TeX>"
Např. to m v kolečku jsem našel díky "latex letters in cicles".
Jo a ještě dodatek: Ten konec jsem psal někdy o půl jedné ráno, takže když ti tam něco bude připadat blbě, je dost dobře možné, že to tak bude. Ale když jsem to psal, tak jsem byl docela přesvědčen, že to takto projde.
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#6 28. 11. 2014 17:15
Re: Mal'cev, Malcev, Maltsev product, součin
↑ OiBobik:
:)
no a při tom všem přemýšlím jenom nad tímto: "jak to víte?"
Nemusíte reagovat.
Tenhle Váš 12.18 příspěvek jsem si teda přečetl celý.
Já se na ten hlavní a krásný první, těším se na to. (fakt jsem nečekal, že se někdo ozve)
OT: Na to TeXování...ano,
po půlhodině hledání texovského "m" v kroužku to vzdávám, budu psát (m), pokud to někdo umíte napsat sem do fóra, prosím
Hledal jsem to stejně tak a našel jsem pár rad, jak se to dělá. Když jsem to ale napsal do toho pole tady vpravo,
pod kterým je napsaný: "Náhled LaTeXového výrazu:" tak se to tam nezobrazovalo správně a nenapadlo mě to i tak zkusit. OK, jsem poučen
Offline
#7 29. 11. 2014 18:55 — Editoval kolejo (29. 11. 2014 20:39)
Re: Mal'cev, Malcev, Maltsev product, součin
↑ OiBobik:
Nebudu zakládat nové téma k projednání (m)-idempotentů.
Dodám to ke svému prvnímu zamyšlení ↑ kolejo:
Buď S v pseudovarietě pologrup na levé straně (to s tím generováním je důležitá věc, kterou jsem si neuvědomoval) je Sl-homomorfismus do polosvazu T. Úplně všechny prvky T jsou idempotentní, proto
je Sl-homomorfismus do polosvazu T. Úplně všechny prvky T jsou idempotentní, proto
Buď a,b nějaké prvky polosvazu T takové, že a je nad b.
EDIT: pak áčka a béčka beru z A a B. A,B jsou pologrupy, které jsou vzory nějakých dvou prvků z T.
[škrtnutý text]Označím pak A a B množiny, které se zobrazují na prvky "a" a "b" respektive.[/škrtnutý text]
//(však si rozumíme) čímž chci říct, že součin dvou prvků "půjde dolů"
čímž chci říct, že součin dvou prvků "půjde dolů"
Proto platí:  a B je polosvaz, takže máme
a B je polosvaz, takže máme 
Ale ještě nevíme, jestli 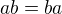 , víme
, víme 
A to je třeba ověřit. (je potřeba to ověřit ještě toto: a*ab=ab*a, b*ab=ab*b ? ono to je stejně docela zřejmý, no)
První sada:
Druhá sada:
Celkem:
Takže tamto S je taky polosvaz a máme hotovo.
Offline
#8 29. 11. 2014 20:27 — Editoval OiBobik (29. 11. 2014 20:58)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Mal'cev, Malcev, Maltsev product, součin
↑ kolejo:
To vypadá správně... Pokud jsem teda pochopil správně, že v jednu chvíli jsi změnil značení a začal chápat  jako prvky
jako prvky  místo toho, aby to označovalo
místo toho, aby to označovalo  jako na začátku. Myslím, že ty věci typu "a*ab=ab*a, b*ab=ab*b" ti vypadnou tak nějak zadarmo, když už máš tu komutativitu (ne?).
jako na začátku. Myslím, že ty věci typu "a*ab=ab*a, b*ab=ab*b" ti vypadnou tak nějak zadarmo, když už máš tu komutativitu (ne?).
BTW: Taky bych řekl, že pokud chce člověk ověřit neplatnost té druhé inkluze, začít s nějakou idempotentní pseudovarietou bude dobrý start (tím si ovšem nejsem vůbec jist).
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#9 29. 11. 2014 20:33
Re: Mal'cev, Malcev, Maltsev product, součin
↑ OiBobik:
Jo, pochopil jste to správně... a, b \in T jsem asi ani nemusel zavádět, stačilo říct A,B vzory dvou prvků T a...tak.
Jdu to tam trochu opravit.
Díky
No a tak áčka patří A, béčka B. A,B jsou polosvazy. a*b jsou v B, b*a je B, ale nevím, jestli se a*b=b*a.
To jsem ověřil a pak asi potřeba ověřit, že i prvek a*b komutuje se všemi prvky z A.
Už to vidím, to b*ab=ab*b je zdarma.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Mal'cev, Malcev, Maltsev product, součin (TOTO TÉMA JE VYŘEŠENÉ)