Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#8 02. 12. 2014 13:24 — Editoval vlado_bb (02. 12. 2014 13:26)
Re: Integrál
Pozri si v nejakej knihe ako sa robi substitucia. Nie tu na tomto fore, nie v Google ani MAW ani nicom podobnom. Nesnaz sa nauzit matematiku metodou nahodnych pokusov. Zober si knihu, poznamkovy zosit a pusti sa do toho. Pocitac zatial vypni.
Offline
#10 03. 12. 2014 21:34
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Integrál
Zdravím,
ještě k zadání - závorky jsou pravděpodobně tak 
Tady můžeš postupně používat substituce, jelikož funkce obsahuje v sobě další složené.
Substitucia moze byt
,
,
?
může, z toho máš  . Můžeš pokračovat další substituci
. Můžeš pokračovat další substituci  , nebo rovnou
, nebo rovnou  . Je ještě něco nejasné? Děkuji.
. Je ještě něco nejasné? Děkuji.
Offline
 ?
? ?
?
 , potom tam bude vystupovat
, potom tam bude vystupovat  co je akurat diferencial zo
co je akurat diferencial zo 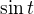 . Cize uplne klasicka skolska uloha na substitucie. Pri troske namahy to ide z hlavy.
. Cize uplne klasicka skolska uloha na substitucie. Pri troske namahy to ide z hlavy. což vede na "tabulkový" integrál
což vede na "tabulkový" integrál ?
?