Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 10. 12. 2014 18:31
- kafe_arabica
- Příspěvky: 38
- Reputace: 3
Izomorfizumus grúp automorfizmov
Ahoj.
Majme priestor  (množinu alebo topologický priestor) a jeho grupu automorfizmov
(množinu alebo topologický priestor) a jeho grupu automorfizmov  . Podobne,
. Podobne,  a
a  . Ak existuje izomorfizmus priestorov
. Ak existuje izomorfizmus priestorov 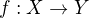 (v zmysle bijekcie alebo homeomorfizmu), môžeme skonštuovať izomorfizmus príslušných grúp automorfizmov;
(v zmysle bijekcie alebo homeomorfizmu), môžeme skonštuovať izomorfizmus príslušných grúp automorfizmov;  ,
,  .
.
Dá sa táto konštrukcia obrátiť? Tzn., ak poznáme izomorfizmus grúp, môžeme skonštruovať izomorfizmus priestorov?
Ide to v nejakých špeciálnych prípadoch, napr. ak ide o nejaké variety (ľubovolného rozmeru)? Resp. dá sa takýto morfizmus skonštruovať, ak pridáme nejaké ďalšie predpoklady. Tým myslím, že by nešlo len o izomorfizmus grúp ale napríklad aj o homológie a iné invarianty?
Offline
#2 10. 12. 2014 20:25
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Izomorfizumus grúp automorfizmov
↑ kafe_arabica:
Ahoj,
tohle je taková neodpověď, ale tak budiž.
Co se množin týče:
Nejprve konečné množiny. Tam to platí s jedinou výjimkou, a sice  . Nicméně dál už je to ok, pro
. Nicméně dál už je to ok, pro  konečnou neprázdnou množinus
konečnou neprázdnou množinus  je
je  , tedy
, tedy  , přitom
, přitom  , JInak řečeno: Bijekce / isomorfismus na automorfismech ti stačí k tomu, rozeznat, zda existuje bijekce na původních množinách.
, JInak řečeno: Bijekce / isomorfismus na automorfismech ti stačí k tomu, rozeznat, zda existuje bijekce na původních množinách.
Nekonečné množiny: Tady nevím, ale tipl bych si, že to nebude rozhodnutelné v ZFC.
Co se topologických prostorů týče:
Tam to určitě neprojde. Např.  kde otevřené množiny jsou
kde otevřené množiny jsou  má automorfsmus jediný, a sice identitu. Totéž ovšem platí i pro jednoprvkový topologický prostor, a tyto dva určitě nejsou homeomorfní.
má automorfsmus jediný, a sice identitu. Totéž ovšem platí i pro jednoprvkový topologický prostor, a tyto dva určitě nejsou homeomorfní.
Ohledně těch dalších invariantů, to taky moc nevím, ale přijde mi to dost nepravděpodobné (už jen proto, že homotopie a homologie zachovávají informaci jen o "pěkných", tj. křivkově souvislých, částech prostorů; tj. když se budu bavit o prostorech, kde např. každé spojité zobrazení z intervalu je konstantní, moc homotopií tam nevykouzlím). Spíš asi je lepší snaha se omezit např. na ty topologické variety. K tomu taky nevím nic moc, ale možná by tě mohl zajímat pojem "rigid topological spaces", tak na to aspoň dávám odkaz.
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline