Matematické Fórum

kafe_arabica

Ahoj.

Môže mi, prosím, niekto vysvetliť ako sa tenzory v matematike prakticky používajú?
Je mi jasné, že napríklad v diferenciálnej geometrii sa hodí Riemannov tenzor, ale ja myslím skôr z definície tenzorového súčinu. Majme dva moduly alebo vektorové priestory $A, B$ (z čoho sa to jednoduchšie vysvetlí), ich tenzorový súčin $A\otimes B$ , kde vzniká bilineárne zobrazenie $\otimes:A\times B\to A\otimes B$ . Ďalej mi je jasné, že bilineárne zobrazenia z $A\times B\to C$ , kde C je ďaľší modul (v.p.) sa faktorizujú podľa zobrazenia $\otimes$ .
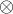Ale niekde som počul, že prvky priestoru $A\otimes B$ nejako pôsobia ... ?
V definícii http://en.wikipedia.org/wiki/Coalgebra# … definition je to tiež nejako zašifrované, lebo rovnosť 1. predpokladá, že $id_C\otimes \Delta$ je zobrazenie $C\otimes C \to C\otimes C\otimes C$ , čo nejako nevidím.
Viete mi to niekto objasniť? Ďakujem.

OiBobik

↑ kafe_arabica:

Ahoj,

to jsem teď nedávno sepisoval, tak ať to využiju co nejvíce...

Nějaká motivace, k čemu je tensorový součin přes tu modulářskou definici dobrý, a jak se časo používá:

Značme množinu zobrazení mezi množinami $X$ a $Z^Y$ , kde ta druhá množina značí množinu všech zobrazení z $Y$ do $Z$ .
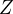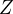Tak stačí jen trocha představivosti k tomu, aby člověk poznal, že je to v podstatě totéž, jako zkoumat množinu zobrazení z $X\times Y$ do $Z$ (identifikace je daná jako $f(x,y)\equiv [f(x)](y)$ ). Takže místo něčeho jako $\mathrm{Map}(X,\mathrm{Map}(Y,Z))$ (kde $\mathrm{Map}(-,-)$ značí množinu všech zobrazení) můžeš pracovat s $\mathrm{Map}(X \times Y, Z)$ , tj. $X\times Y$ je opět množina, že ve zobrazeních z ní jsou "zakódována" zobrazení z $X$ do (zobrazení z $Y$ někam).

Když to řeknu trochu vznosně, tak máme (přirozený) isomorfismus v kategorii množin

No a teď zkusme tomu udělat formální analogii v kategorii $R$ -modulů (pro jednoduchost nechť je $R$ komutativní). Tak to je přesně to, na co je tensorový produkt dobrý. Máme
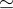$\mathrm{Hom}_R(U, \mathrm{Hom}_R(V,W)) \simeq \mathrm{Hom}_R(U\otimes_RV, W)$ , kde $\mathrm{Hom}_R(-,-)$ značí vzít grupu (zde dokonce $R$ -modul) všech homomorfismů mezi příslušnými moduly, a $\simeq$ značí grupový (zde dokonce $R$ -modulový} isomorfismus.

Tohle je jedna y klíčových vlastností tensorového součinu (říká se tomu tensor-hom adjunkce) a používá se to docela často (i když samozřejmě záleží na tom, co děláš). Jinak mezi další využití patří např.

komplexifikace vektorového prostoru:
Máme-li reálný vektorový prostor a chceme jej považovat za komplexní vektorový prostor, univerzální možnost, jak jej změnit, je jej komplexifikovat: místo $V$ uvažovat $V \otimes_{\mathbb{R}}\mathbb{C}$ . Má to třeba tu dobrou vlastnost, že reálná dimenze $V$ je komplexní dimenze $V \otimes_{\mathbb{R}}\mathbb{C}$ .

"zvektorovatění" abelovské grupy:
Máme-li abelovskou grupu $A$ a chceme ji chápat jako vektorový prostor nad tělesem $K$ , zcela analogicky je nejpřirozenější volba $A \otimes_\mathbb{Z}K$ (každá abelovská grupa je 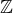$\mathbb{Z}$ -modul, dokonce jediným způsobem, a každé těleso je 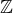$\mathbb{Z}$ -algebra tímtéž způsobem).

lokalizace grupy /modulu:
Opět jde o něco podobného, tj. např. představ si, že chceš v abelovské grupě $A$ dělit nějakým celým číslem, třeba $3$ . Tak si vezmeš "lokalizaci 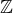$\mathbb{Z}$ mimo $3$ ", tj. $(\mathbb{Z})_3=\{\frac{a}{3^k}\: | \; k \in \mathbb{N}, a \in \mathbb{Z}\}$ , což je podokruh $\mathbb{Q}$ , a uděláš $A \otimes_{\mathbb{Z}}(\mathbb{Z})_3$

No a nějaký cool příklad na závěr:
Představ si, že máš nějakou dostatečně hezkou kompaktní plochu, že na ní můžeš zavést strukturu hladké variety (tj. kompaktní Riemannovu plochu), zna4me ji $X$ . Pak má-li člověk dva vektorové bandly nad tou plochou, může udělat jejich tensorový součin, výsledek je opět vektorový bandl. Dívejme se na line bundly, tj, bandly dimenze $1$ . Ty jsou zřejmě uzavřeny na tensorový součin bandlů. Fór je v tom, že triviální badndl $\mathbb{C}\times X \rightarrow X$ je neutrální prvek vůči tensorovému součinu, ve smyslu $L \otimes (\mathbb{C} \times X) \simeq L$ . Dá se pak ukázat, že množina všech line bundleů na $X$ modulo isomorfismus bandlů má strukturu grupy, jde o tzv. Picardovu grupu Riemannovy plochy $X$ . Jde o dost důležitý invariant (který má analogii např. i na algebraických křivkách - struktura této grupy je v podsatě totéž, co ona slavná grupová struktura na eliptických křivkách).

Co se těch koaleber týče, to moc neznám, ale tam bude asi následující zrada: z kontextu to vypadá, že 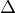$\Delta$ bude (v tom základním příkladu) diagonální zobrazení, tj. něco jako $C \rightarrow C \otimes C$ , $c \mapsto c \otimes c$ . Což asi obecně nebude $K$ -lineární - nicméně, jak je vysvětleno v příkladu hned pod defincí, asi má jít o lineární zobrazení, které se definuje $b \mapsto b \otimes b$ na bázi a pak se to lineárně rozšíří.

Matematické Fórum

#1 06. 10. 2014 10:17 — Editoval kafe_arabica (06. 10. 2014 10:21)

Význam tenzorov

#2 12. 12. 2014 17:24 — Editoval OiBobik (12. 12. 2014 18:27)

Re: Význam tenzorov

Zápatí