Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Meze trojného integrálu (TOTO TÉMA JE VYŘEŠENÉ)
#1 13. 12. 2014 10:52
Meze trojného integrálu
Zdravím, měl bych pár příkladů u kterých potřebuji pomoci nebo si jen ověřit, že je to správně:
1.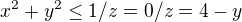 zadání příkladu
zadání příkladu
Provedl jsem transformaci do polárních souřadnici a vyhodnotil tyto meze. (Jsou v pořádku?)
2. ![kopírovat do textarea $[0;0],[1;0],[0;3]$](/mathtex/16/169c9b52ad194ec948afe7d4854e18a6.gif)
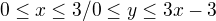
3.Tady si nevím rady odkud vede Z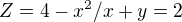
čili meze jsem udělal: 
Děkuju za jakoukoliv radu. Hlavně s tím Z v posledním příkladě bych potřeboval poradit.
Offline
- (téma jako vyřešené označil(a) jelena)
#2 13. 12. 2014 11:25
- Argcotgh x
- Příspěvky: 230
- Škola: MFF UK
- Pozice: student
- Reputace: 5
Re: Meze trojného integrálu
ad 1) meze ró a fí myslím v pořádku, se z si nejsem jistý. Po transformaci souřadnic nezapomeň přidat do integrandu jakobián.
Offline
#3 13. 12. 2014 13:26
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Meze trojného integrálu
Zdravím,
↑ Redstar: nedávej, prosím, do tématu více dotazu viz pravidla (pokud to není jen ukázka úloh a potřebuješ např. odkaz na studijní materiál).
1. mi vyšla stejně, jen to jsou souřadnice válcové,
2. pokud je úloha v rovině, potom je zadán pravoúhlý trojúhelník (meze ovšem nejsou dobře, zkus ho pořádně nakreslit), v prostoru by to zadávalo nekonečny hranol s trojúhelníkovou podstavou (tak se ještě podívej na zadání)
3. tam není ani jasné, kam vede z (bude lepší nový dotaz, kompletní zadání + jednotlivé řádky pro podmínky od sebe oddělit (jinak Tvůj zápis spíš vypadá jako zlomek 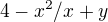 s "nejasným" jmenovatelem.
s "nejasným" jmenovatelem.
Děkuji.
Offline
#4 13. 12. 2014 13:56
Re: Meze trojného integrálu
↑ jelena:
Zdravím, tak to se omlouvám, je to už nějaký ten pátek co sem tady vůbec něco psal. Přišlo mi to logické když jde o stejnou věc :-). No nicméně mám to nechat už tak nebo rozdělit ?
1. Ano válcové souřadnice, nemohl jsem si vzpomenou, každopádně jsem rád, že se chápeme :-)
2. Jedná se o Dvojný integrál v obecné oblasti (nikoliv trojný, chyba zápisu), otázkou tedy víceméně je, jen jestli je dobře napsaný ten směrnicový tvar přímky ? Dá se na něj přijít jednodušší metodou nebo nutně pomocí tohoto vzorce 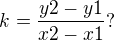
A otázkou je, který bod je pro mě 1 a který 2 ? Záleží na pořadí nebo to výjde stejně ?
3. K tomu tedy vytvořím zvlášť topic.
Děkuju za pomoc.
Offline
#5 13. 12. 2014 14:15
- Argcotgh x
- Příspěvky: 230
- Škola: MFF UK
- Pozice: student
- Reputace: 5
Re: Meze trojného integrálu
ad 2)
řekl bych, že x jde od 0 do 1 a ypsilon od 0 do (-3x+3) - oblast shora ohraničuje přímka y = - 3x + 3
(lze spočítat jednoduše ze 2 bodů, tj. [0;3] a [1;0]
Pak by to mělo vyjít
∫ (od 0 do 1) ∫ (od 0 do -3x+3) dy dx = ∫ (od 0 do 1) -3x + 3 dx = [-3/2 x^2 + 3x] (od 0 do 1) =
= -3/2 + 3 - 0 + 0 = 3 - 3/2 = 3/2
Když se to tak ale vezme, tak to lze spočítat triviální geometrickou úvahou, zcela bez integrálů: ty 3 body ohraničují pravoúhlý trojúhelník a jeho obsah je 1/2*a*b = 1/2 * 1 * 3 = 3/2.
Offline
#6 13. 12. 2014 15:15
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Meze trojného integrálu
↑ Redstar:
děkuji, určitě nové téma bude přehledné. Předpis lineární funkce můžeš spočítat každou metodou - kolega ↑ Argcotgh x: navrhuje pravděpodobně řešení soustavy rovnic  s využitím 2 zadaných bodů. Směrnice bude vycházet, pokud odpovídajícím y budou souhlasit jejich x (ne přehozené), spíš z praktického hlediska bereme indexy pro x zleva napravo po číselné ose, k tomu přiřadíme odpovídající y.
s využitím 2 zadaných bodů. Směrnice bude vycházet, pokud odpovídajícím y budou souhlasit jejich x (ne přehozené), spíš z praktického hlediska bereme indexy pro x zleva napravo po číselné ose, k tomu přiřadíme odpovídající y.
↑ Argcotgh x: ano, děkuji, geometrická interpretace je dobrá kontrola, děkuji, jen by kolega mohl upřesnit, co v zadání
Jedná se o Dvojný integrál v obecné oblasti
znamená "obecná oblast" + zda je požadavkem výpočet obsahu obrazce vymezeného body, nebo něco jiného.
Offline
#7 13. 12. 2014 15:36
- Argcotgh x
- Příspěvky: 230
- Škola: MFF UK
- Pozice: student
- Reputace: 5
Re: Meze trojného integrálu
Abych pravdu řekl, rovnici přímky ze 2 bodů počítám pomocí determinantu:
| x1, y1, 1 |
| x2, y2, 1 | = 0
| x, y, 1|
Kde se dosadí A (x1, y1) a B (x2, y2), x,y se při výpočtu berou jako "symboly". Determinant jednoduše podle Sarrusova pravidla.
Možná to vypadá, že "beru kanón na vrabce", ale přijde mi to skoro jednodušší než se párat s normálovými vektory apod.
Offline
#8 14. 12. 2014 12:06
Re: Meze trojného integrálu
↑ jelena:
Děkuji moc za radu. S integrály už nemívám problém. Ano jedna se o výpočet obsahu. Snažím se pouze dobře zjišťovat meze. Bez nich totiž nejede vlak, že ano :-). Takže jestli to chápu dobře, tak je jedno jestli dosadím do vzorce
za ![kopírovat do textarea $[x_{1},y_{1}] $](/mathtex/b5/b572a09cc10cccad6bdbd52608de4d4f.gif) bod
bod ![kopírovat do textarea $[1,0] nebo [0,3] $](/mathtex/9f/9fd3adfeed279645720fe6bfc46e6293.gif)
Hlavní je tedy, aby zůstaly x odpovídaly jejich y.
Offline
#9 14. 12. 2014 17:20
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Meze trojného integrálu
Hlavní je tedy, aby zůstaly x odpovídaly jejich y.
ano, je to jedno, důležité nepřehodit jednotlivé souřadnice u bodů. Jinak osobně bych volila cestu ZŠ, zapíšu, že přímka bude ve tvaru  a jednou za x, y dosadím bod
a jednou za x, y dosadím bod ![kopírovat do textarea $[1,0]$](/mathtex/91/91a3ccdf14346c86322c0b6d2675b569.gif) , potom
, potom ![kopírovat do textarea $[0,3]$](/mathtex/74/74fdd9b15a3b8f946faea886ca7ae003.gif) a najdu neznámé a, b (je to někde na konci sbírky Bělouna).
a najdu neznámé a, b (je to někde na konci sbírky Bělouna).
Zbytek je asi vyřešen.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Meze trojného integrálu (TOTO TÉMA JE VYŘEŠENÉ)
