Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 18. 12. 2014 09:20
- Crashatorr
- Příspěvky: 360
- Reputace: 7
Konvergence řady
Zdravím, mohl by mi někdo poradit jak na tento příklad? Řady jsme zatím vvůbec nedělali
Offline
- (téma jako vyřešené označil(a) Crashatorr)
#2 18. 12. 2014 09:57
Re: Konvergence řady
ak je to tak ako to je napísané tak pre kladné n je to nekonečno pre záporné n je to mínus nekonečno a pre nulové n je to nula
ale skôr by bolo podľa mňa zaujímavejšie uvažovať
potom
MATH IS THE BEST!!!
Offline
#3 18. 12. 2014 11:57
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Konvergence řady
Zdravím,
↑ jarrro: mohu dotaz - zde před krátkou dobou kolega hledal jiný postup řešení pro typy  (jako v tématu), přidala jsem výběr z místních zdrojů a nejen - derivování je "první volba". Jsou jiné postupy, nebo je to složitější na použití a je zbytečné si vymýšlet?
(jako v tématu), přidala jsem výběr z místních zdrojů a nejen - derivování je "první volba". Jsou jiné postupy, nebo je to složitější na použití a je zbytečné si vymýšlet?
Děkuji.
Offline
#6 18. 12. 2014 13:50 — Editoval Pavel (18. 12. 2014 13:51)
Re: Konvergence řady
↑ jelena:
Existují jednodušší metody, jak tyto sumy počítat bez použití derivací. Stačí základní znalosti diferenčního počtu týkající se řešení linearních diferenčních rovnic 1. řádu se speciální pravou stranou a je potřeba umět pracovat s limitami.
Definujme posloupnost  předpisem
předpisem
Pak zřejmě 
Jedná se tedy o lineární diferenční rovnici s nehomogenní pravou stranou a počáteční podmínkou. Dá se ukázat, že řešení rovnice lze vyjádřit ve tvaru:
Součet zadané nekonečné řady se pak určí limitním přechodem, tj.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#7 18. 12. 2014 18:01
- check_drummer

- Příspěvky: 5181
- Reputace: 106
Re: Konvergence řady
Pavel napsal(a):
Dá se ukázat, že řešení rovnice lze vyjádřit ve tvaru:
Ahoj, a existuje také nějaký způsob, jak na ten vzorec přijít? Protože když už ho máme, tak ten důkaz, že jde o řešení bude o mnoho snadnější...
"Máte úhel beta." "No to nemám."
Offline
#8 18. 12. 2014 18:51 — Editoval Pavel (18. 12. 2014 18:57)
Re: Konvergence řady
↑ check_drummer:
Ten vzorec vychází jako řešení příslušné diferenční rovnice. Pokud využijeme poznatků z teorie diferenčních rovnic, tak v případě rovnice
kde  ,
,  je reálný polynom
je reálný polynom  -tého stupně a
-tého stupně a 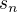 je
je  -tý člen hledané neznámé posloupnosti
-tý člen hledané neznámé posloupnosti  , má řešení této diferenční rovníce, tj. předpis pro
, má řešení této diferenční rovníce, tj. předpis pro 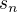 , tvar
, tvar
kde  je libovolná reálná konstanta a
je libovolná reálná konstanta a  je polynom stejného stupně jako zadaný polynom
je polynom stejného stupně jako zadaný polynom  , přičemž koeficienty polynomu
, přičemž koeficienty polynomu  se určí tak, aby diferenční rovnice byla splněna, tj. "aby vyšla zkouška správnosti". Konstanta
se určí tak, aby diferenční rovnice byla splněna, tj. "aby vyšla zkouška správnosti". Konstanta  se určí tak, aby byla splněna počáteční podmínka.
se určí tak, aby byla splněna počáteční podmínka.
Bude-li  , pak pro součet nekonečné řady platí
, pak pro součet nekonečné řady platí
je-li 
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#9 18. 12. 2014 23:45
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Konvergence řady
Zdravím,
↑ Pavel: děkuji velice, bohužel teorii diferenčních rovnic ovládám ještě hůř, než teorii řad (kterou také ovládám jen v úplných základech), diferenční rovnici (některou) dokážu jen mechanicky spočítat pomocí Z-transformace.
Tak bych patrně v tématu jen překážela vaši debatě :-), ale kolegu v dalším tématu poinformuji. Ještě jednou děkuji.
Offline
#10 19. 12. 2014 11:31 — Editoval Rumburak (19. 12. 2014 11:39)
Re: Konvergence řady
↑ Pavel:
Ahoj.
Může být ovšem tématem do diskuse, která z uvažovaných metod (přes diferenciální rovnice či přes diferenční
rovnice) je technicky jednodušší. :-)
Také mám dojem, že diferenční rovnice bývají zahrnuty do osnov VŠ méně často než rovnice diferenciální .
Offline
#11 19. 12. 2014 11:48
Re: Konvergence řady
↑ Rumburak:
To je samozřejmě pravda. Na jednu stranu řešení pomocí diferenčních rovnic nevyžaduje použití derivací, stačí určit koeficienty neznámého polynomu, což po úpravě vede na řešení soustavy lineárních rovnic. Na druhé straně nevýhoda diferenčních rovnic spočívá v tom, že pomocí ní nelze takto jednoduše najít např. součet nekonečné řady
Derivace a integrály jsou v tomto případě mnohem efektivnější.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline

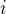 .
. malo byt
malo byt