Matematické Fórum

Kouří se mi v hlavě · 30. 12. 2014 20:28

Ahoj,

potřeboval bych zkontrolovat postup výpočtu, mrkli byste mi na to prosím?

Zadání: $f(x)=\frac{1}{2}\cdot (x+\frac{1}{x})$
1) Definiční obor: $D=\mathbb{R}\setminus \{0\}$
2) Není sudá, je lichá – platí: $f(-x)=-f(x)$
3) Není periodická, zkoušeno na $t=1$ a x=1, neplatí: $f(x+t)=f(x)$ (víc jsem nezkoušel a nevím, jestli stačí tento příklad a zapojení selského rozumu)
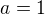4) Funkce je spojitá, platí vztah: $\lim_{x\to a}f(x)=f(a)$ (Tvrdím na základě platného $a=1$ , stačí to?)
5) Body nespojitosti, x=0:
a) $\frac{1}{2}\lim_{x\to 0^{+}}(x+\frac{1}{x})=0$
b) $\frac{1}{2}\lim_{x\to 0^{-}}(x+\frac{1}{x})=0$
>> existuje oboustranná limita a to 0, tzn. v bodě 0 je funkce nespojitá?
6) Průsečík s osou x: 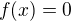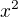$f(x)=0$ $\Rightarrow x^{2} + 1 0$ , $x^{2}$ je vždy kladné nebo 0, tzn. vztah neplatí a průsečík s osou x neexistuje? Tzn. že nelze určit, kdy je funkce kladná nebo záporná?
7) Průsečík s osou y: $x=0 \Rightarrow \frac{1}{2}\cdot (0+\frac{1}{0})$ , nedefinovaný výraz v oboru reálných čísel, tzn. neexistuje průsečík s osou y?
8) První derivace: $\frac{1}{2}\cdot (1-\frac{1}{x^{2}})$ (správně podle WolframAlphy, nejistý jsem si ale s extrémy)
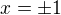9) Extrémy a monotonie: $f(x)' = 0$ , vyšlo: $x=\pm 1$ , s nulou z definičního oboru první derivace mám 4 intervaly: $(-\infty ,-1>,<-1,0),(0,1>,<1,+\infty )$ , na všech mi vyšlo, že je funkce rostoucí, tzn. je bez extrémů?
10) Druhá derivace: $f''(x)=\frac{1}{x^{3}}$ (správně podle WolframAlphy, nejistý jsem si dál)
11) $\frac{1}{x^{3}} >0$ , pro x>0 platí 1>0 ... pro x < 0 platí 1<0, platné výrazy, tzn. funkce je konvexní?
Pro konkávní funkci neexistuje platný výraz... a tedy jsem nenašel inflexní body, je to možný?

Díky za pomoc.

Jj · 30. 12. 2014 20:52

↑ Kouří se mi v hlavě:

Dobrý den.

Zhruba:

Ad 4, 5 - funkce je spojítá pro x < 0, x > 0

limity v bodě 5 nejsou dobře.

Ad 6 - průsečíky s osou x nejsou, ale pro x < 0 je f(x) < 0, pro x > 0 je f(x) > 0

Ad 7 - průsečíky s osou y nejsou

Ad 9 - není všude rostoucí, v intervalech <-1,0), <1, infty) je klesající.

podezřelé body pro extrémy jsou x = +-1 (1. derivace je = 0), dořešit pomocí druhé derivace

Ad 10 - v jednom intervalu konkávní, v druhém konvexní

Ad 11 - podle mě nemá inflexní body

Schází asymptoty - podívat se na bod x = 0 a dále na tvar předpisu funkce (případně spočítat šikmou asymptotu pomocí příslušných limit).

misaH · 30. 12. 2014 20:59

↑ Kouří se mi v hlavě:

Ahoj.

Pre predstavu si môžeš nechať vykresliť graf (WA, MAW, Geogebra, ...).

Kouří se mi v hlavě · 30. 12. 2014 22:11

↑ misaH:

Ahoj,
díky, koukám na to :)

↑ Jj:

Dobrý den,
díky moc!

5) Body nespojitosti, x=0:
a) $\frac{1}{2}\lim_{x\to 0^{+}}(x+\frac{1}{x})=\infty$
b) $\frac{1}{2}\lim_{x\to 0^{-}}(x+\frac{1}{x})=-\infty$

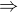$\Rightarrow$ bod 0 je bod nespojitosti 1. druhu ?

9) Překontroloval jsem si to, pro interval <-1,0) mi funkce vyšla skutečně klesající, ale už mi to nevychází pro <1, infty) .. to mi vychází pořád kladně, je to možné?

10) $\frac{1}{x^{3}} > 0$ (podmínka pro funkci konvexní)
- rozpadne se mi to na dvě větve, kdy x> 0 a kdy x <0, platí výraz pro x>0, kdy 1 > 0 je platným výrazem a tedy pro $x>0$ je funkce konvexní

$\frac{1}{x^{3}} < 0$ (podmínka pro funkci konkávní)
- rozpadne se mi to na dvě větve, platí jedna z nich a to x<0, kdy 1 > 0 je platný výraz
tedy pro $x<0$ je funkce konkávní, je to tak?

Moc děkuju, jdu se ještě pustit do těch asymptot.. :)

Jj · 30. 12. 2014 22:37

↑ Kouří se mi v hlavě:

Ad 5 - zřejmě nepůjde o nespojitost prvního druhu (jednostranné limity obě konečné), ale druhého druhu (aspoň jedna je nevlasní nebo neexistuje).

Ad 9 - ano - v tom bodě jsem se sekl - pro <1, infty) je rostoucí, klesající pro (0, 1>.

Kouří se mi v hlavě · 30. 12. 2014 23:07

↑ Jj:

ad 5) jo, tak podle té definice by to pak sedělo :)

ad 9) díky, taky mi to už sedí

10) konkávnost a konvexnost jsem určil dobře?

12) Asymptoty:
Funkce má symptoty bez směrnice: $x=0$ (svislá asymptota)
- na základě i 5)

Šikmé asymptoty:
a) v $+\infty$ : $\frac{1}{2}\lim_{x\to \infty }\frac{\frac{x^{2}+1}{x}}{x}=\frac{1}{2}\lim_{x\to \infty }(x^{2}+1) =\infty$
>> v nekonečnu nemá funkce šikmou asymptotu

b) v $-\infty$ : $\frac{1}{2}\lim_{x\to -\infty }(x^{2}+1) =\infty$
>> v mínus nekonečnu nemá funkce šikmou asymptotu

Je to správně?

Zapomněl jsem na extrémy:
Lmax = [1,1]; Lmin [-1,-1] ... to by sedělo, souhlasíte?

Předem moc děkuju za potvrzení.

Jj · 30. 12. 2014 23:25 — Editoval Jj (30. 12. 2014 23:26)

↑ Kouří se mi v hlavě:

Ad 10 - ano, správně.

Ad 12 - svislá asymptota srpávně, šikmá chyba:

Pouvažujte nad předpisem funkce $f(x)=\frac{1}{2}\cdot \left(x+\frac{1}{x}\right)$

při rostoucím x se f(x) blíží k přímce y = x/2, při klesajícím x k přímce k téže přímce "na druhém konci"

Takže by měla být šikmá asymptota y = x/2 a výpočty v bodě 12 nebudou v pořádku.

Extrémy správně.

Kouří se mi v hlavě · 30. 12. 2014 23:45

↑ Jj:

Moc děkuju, ještě se chci zeptat, lze nějak početně dojít k tomu, že nemá funkce inflexní body? Resp. stačí prohlásit, že pro výraz $\frac{1}{x^{3}}=0$ nemá x kořeny?

Jj · 31. 12. 2014 10:38 — Editoval Jj (31. 12. 2014 10:41)

↑ Kouří se mi v hlavě:

Pokud vím, tak podmínka f''(x) = 0 je nutná podmínka pro existenci inflexního bodu. Takže ano - bez jejího splnění inflexní bod na grafu není.

Kromě této nutné podmínky je ještě třeba, aby f''(x) měnila v uvedeném bodě znaménko.

Pavel · 31. 12. 2014 14:52 — Editoval Pavel (31. 12. 2014 15:24)

↑ Jj:

Pozor! Ta podmínka f''(x) = 0 je nutná pouze v případě, že v inflexním bodě f''(x) existuje. Inflexní bod může mít funkce f i v bodě, kde f''(x) neexistuje.

Jj · 31. 12. 2014 15:36

↑ Pavel:

Díky.

Kouří se mi v hlavě · 31. 12. 2014 18:30

↑ Jj:

Díky.

↑ Pavel:

Jsem z toho dost zmatený.

pouze v případě, že v inflexním bodě f''(x) existuje

Jak dojdu k tomu, že v inflexním bodě existuje funkce druhé derivace, když nevím, jaký je inflexní bod?

Inflexní bod může mít funkce f i v bodě, kde f''(x) neexistuje.

Kdyby tohle nastalo, tak bych vyšetřoval extrémy první derivace? Resp.

Inflexní bod = Bod (x, y) funkce f(x), ve kterém má první derivace f′(x) extrém, tj. (lokální) minimum nebo maximum (není to totéž jako tvrzení, že y má extrém).

Když jsou extrémy mé funkce Lmax = [1,1]; Lmin [-1,-1] jsou to tedy i inflexní body?

Moc dík.

Pavel · 31. 12. 2014 18:52

↑ Kouří se mi v hlavě:

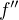Jednoduše řečeno, nejdříve je potřeba najít všechna řešení rovnice $f''(x)=0$ , v nichž je funkce f definovaná, a k nim přidat také ty body, v nichž je funkce f sice definovaná, ale $f''$ neexistuje.

Pak z těchto "kandidátů na inflexní bod" je třeba vybrat ty, na jejichž okolí se funkce f mění z konvexní na konkávní, nebo naopak, a ty jsou pak inflexními body funkce f.

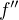Příklad funkce, která má inflexní bod v bodě $x_0$ , v němž $f''$ neexistuje, je $f(x)=x\cdot|x|$ , $x_0=0$ , nebo $g(x)=\sqrt[3]{x}$ , $x_0=0$ .