Matematické Fórum

mb305 · 02. 01. 2015 20:07

Ahoj,

analyzuji funkci .

1/ Definiční obor jsem určil jako všechna reálná čísla (podmínka platí pro celý obor R).

2/ Obor hodnot - zde jsem narazil na problém při vyjádření proměnné . Můj postup: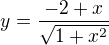
$y = \frac{-2 + x}{\sqrt{1+x^2}}$
$y*\sqrt{1+x^2} = x - 2$
$y^2* (1+x^2) = x^2 - 4x + 4$
$x^2y^2 - x^2 + 4x = 4 - y^2$
$x^2(y^2 -1 + \frac{4}{x}) = 4 - y^2$
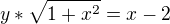
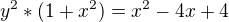
Nevím jak nyní vyjádřit samotné $x$ .

Pavel · 02. 01. 2015 20:26

↑ mb305:

Doporučuji najít globální extrémy funkce f na množině $\mathbb R^*=\mathbb R\cup\{\pm\infty\}$ :-)

Matematické Fórum

#1 02. 01. 2015 20:07

Nalezení oboru hodnot funkce

#2 02. 01. 2015 20:26

Re: Nalezení oboru hodnot funkce

Zápatí