Matematické Fórum

vulkan66 · 05. 01. 2015 19:17

Ahoj, potřebuju poradit se 2. příklady.
//forum.matweb.cz/upload3/img/2015-01/79425_Bez%2Bn%25C3%25A1zvu.png
Můj postup u prvního:

síla, která napíná lano: $F=mg-ma$
moment síly: $N=\frac{dL}{dt}a=\frac{I}{R}a$ a zároveň $N=R*F$
$R*F=\frac{I}{R}a$
za F dosadím: 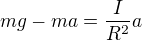$mg-ma=\frac{I}{R^{2}}a$
vyjádřím zrychlení: $a=\frac{mg}{\frac{I}{R^{2}}+m}$
Tady končím. Vůbec nevim jestli je to správný postup.

U druhého vůbec nevim.

Děkuji za pomoc

zdenek1 · 06. 01. 2015 00:02

↑ vulkan66:
K 1)
je to dobře, jen přidáš $I=\frac12MR^2$
Vidíš, že $a=konst.$ , takže je to obyčejný rovnoměrně zrychlený pohyb, takže $v^2=2al$

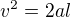
2) Je to obyčejné fyzikální kyvadlo, takže jedna možnost je vybodnout se na nápovědu a někde si najít vztah pro periodu fyz. kyvadla.

A nebo to chceš celé odvodit, pak se můžeš podívat do Encyklopedie fyziky (nahoře na stránce) jak se to dělá.