Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » Bod daných vlastností na parabole (TOTO TÉMA JE VYŘEŠENÉ)
#2 07. 01. 2015 16:20
Re: Bod daných vlastností na parabole
↑ krauva:
Body na parabole budou mít souřadnice vyhovující rovnici  . Hledaný bod pak např.
. Hledaný bod pak např. ![kopírovat do textarea $P\left[\frac{y_0^2}2;y_0\right]$](/mathtex/8b/8b09a71181ef89ea201d18cea0586b1c.gif)
Vzdálenost tothoto bodu od dané přímky je
Tato hodnota bude minimální, když bude minimální čitatel. Kvadratický výraz má záporný diskriminant, tudíž je vždy kladný, takže minimum bude ve vrcholu
dopočítat x-ovou souřadnici by neměl být problém.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#3 07. 01. 2015 16:41
Re: Bod daných vlastností na parabole
↑ zdenek1:
Díky moc za zajímavý postup, jen bych se rád na něco zeptal:
1) může někdy teoreticky u toho výrazu vyjít diskriminant 0 nebo větší a co by to znamenalo?
2) chápu dobře, že si výraz doplníš na čtverec a zjistíš v jaké hodnotě má minimum (nebo jak si přišel na -4/2 ?)
Offline
#4 07. 01. 2015 16:50
Re: Bod daných vlastností na parabole
↑ krauva:
1) jistěže může. Pak to znamená, že výraz nabývá nulové hodnoty. Protože je to celé v abs. hodnotě, ty nulové hodnoty budou minima.
2) doplnění na čtverec je určitě dobrá metoda. Já si ale pamatuju vztah  , kde
, kde  a
a  jsou koeficienty i kvadratického a lineárního členu.
jsou koeficienty i kvadratického a lineárního členu.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#5 07. 01. 2015 17:06
Re: Bod daných vlastností na parabole
↑ zdenek1:
Jestli ještě můžu něco: zkoušel sem to počítat nejprve pro x souřadnici a vyšlo mi, že: (jestli je to teda dobře..?), ta by měla mít minimum v 0 kvůli nezápornosti ale to nesedí pro 1. výpočet
(jestli je to teda dobře..?), ta by měla mít minimum v 0 kvůli nezápornosti ale to nesedí pro 1. výpočet
Dělám něco špatně, nebo se to takhle nedá?
Dík za všechno
Offline
#6 07. 01. 2015 17:55
Re: Bod daných vlastností na parabole
↑ krauva:
Je to dobře jen na půl (takže vlastně není)
když z rovnice paraboly vyjádříš  , tak dostaneš
, tak dostaneš  (proto jsem taky volil obrácené vyjádření)
(proto jsem taky volil obrácené vyjádření)
Takže ten tvůj výraz bude  a dostaneš dvě hodnoty a samozřejmě, ta záporná nebude vyhovovat.
a dostaneš dvě hodnoty a samozřejmě, ta záporná nebude vyhovovat.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » Bod daných vlastností na parabole (TOTO TÉMA JE VYŘEŠENÉ)

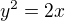 najděte bod, který je nejblíže k přímce p:
najděte bod, který je nejblíže k přímce p: 