Matematické Fórum

jelinekgreen · 07. 01. 2015 21:42

Zdravím, prosím o pomoc s několika limitami.

a) $\lim_{n \to \infty }\frac{n+(-1)^{n}}{n-(-1)^{n}}$

b) $\lim_{n \to \infty }\frac{(-1)^{n}}{n}$

Vůbec to nechápu, protože $(-1)^{n}$ není definováno. Tak jak s těmi limitami dál pracovat?

c) $\lim_{n \to \infty }\frac{(n)^{n}}{n!}$

Tady sice není nic nedefinovaného, ale stejně nevím, co s tím. Resp. L´Hospital, ale wolfram poradil derivaci faktorialu jako součin gamma funkce a bigamma funkce, takže se zřejmě musí najít nějaká úprava a ta mě nenapadá..

Moc děkuju za rady :)

vlado_bb · 07. 01. 2015 21:43

↑ jelinekgreen:Zacnime s bodom a. Skus si par clenov tej postupnosti napisat. Co vidis?

vlado_bb · 07. 01. 2015 21:44

↑ jelinekgreen:A preco by $(-1)^n$ nemalo byt definovane?

jelinekgreen · 07. 01. 2015 21:53

↑ vlado_bb:
Protože $-1^{a}=-1\vee +1$ podle toho, jestli je a sudé nebo liché a jelikož a je nekonečno, tak se neumím rozhodnout? (a protože wolfram se neumí rozhodnout)

jelinekgreen · 07. 01. 2015 21:54

↑ jelinekgreen:
A jako posloupnost to osciluje k jedné polovině?

vlado_bb · 07. 01. 2015 21:56

↑ jelinekgreen:Neviem ako Wolfram, ale ja sa rozhodnut viem, ak je $n$ parne, tak $(-1)^n=1$ , ak neparne, tak $(-1)^n=-1$ .

vlado_bb · 07. 01. 2015 21:57

↑ jelinekgreen:Myslis bod a? Aky je tisici clen? A milionty? Je to priblizne jedna polovica?

jelinekgreen · 07. 01. 2015 22:05

↑ vlado_bb:Pokud teda uvažuju, že je to buď 1 nebo -1, tak proč limita $\lim_{n \to \infty }\frac{1+(-1)^{n}}{2}$ není definovaná? Jestliže $(-1)^{n}$ je buď 1 nebo +1, pak bych uvažoval tu limitu jako $\frac{1+1}{2}$ a nebo $\frac{1-1}{2}$ . Jenže ona není definovaná.

A s tou posloupností nevím. Je to můj tip. Nějak moc jsme s tím nepracovali. S oscilujícími vůbec. Ale řekl bych, skáče-li neustále mezi +1-1+1-1+1-1, tak má průměr vlastně v 0. Aha. No ale v tom případě bych ke, v tomhle příspěvku zmíněné limitě, přidal třetí možnost a to $\frac{1-0}{2}$

Takže jsem zatím zmaten asi jen víc :/

vlado_bb · 07. 01. 2015 22:07

↑ jelinekgreen:Aky je tisici clen tej postupnosti?

jelinekgreen · 07. 01. 2015 22:09

↑ vlado_bb:
1

vlado_bb

↑ jelinekgreen:nie. Postupnosti z bodu a.

jelinekgreen · 07. 01. 2015 22:16

↑ vlado_bb:Jako posloupnost se bere celá ta limita? $\lim_{n \to \infty }\frac{1+(-1)^{n}}{2}$

Takže tisící člen by potom byl $\lim_{n \to \infty }\frac{1+1}{2}$ ? Ale to je taky 1. Tzn. vůbec nechápu.

vlado_bb · 07. 01. 2015 22:27

↑ jelinekgreen:Pozri si to cele od zaciatku v knihe

jelinekgreen · 07. 01. 2015 22:30

↑ vlado_bb: $\lim_{n \to \infty }\frac{1+(-1)^{n}}{2}$ Podle mých skript není definovaná. Zřejmě kvůli tomu výrazu $(-1)^{n}$ . Tak jak s tím můžu jinde pracovat, když tady to nejde, v čem je rozdíl? Popravdě jsem před zkouškou a nemám čas prohlížet skripta sem tam, abych našel odpověď, kterou nevím, kde hledat. Tak trochu jsem doufal, že mi to tu třeba někdo vysvětlí :/

vlado_bb · 07. 01. 2015 22:42

↑ jelinekgreen:To je to iste ako keby si sa opytal, preco vo vyraze 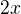$2x$ mozeme pracovat s $x=0$ , ked predsa $\frac 1x$ je v nule nedefinovane. A pokial ide o tu skusku ... ak nevies povedat, co je tisici clen postupnosti z bodu a, tak termin urobenia skusky ta vobec nemusi trapit, je totiz velmi, velmi daleko.

jelinekgreen · 07. 01. 2015 22:54

↑ vlado_bb: Něčemu nerozumím - jsem dement. Fajn. Čemu se teda výraz $(-1)^{n}$ limitně blíží? A k posloupnosti - já jsem do teď nepochopil, o jaké mluvíš. Napiš mi, prosím, přesný předpis posloupnosti, pro kterou chceš, abych ti řekl tisící člen. Že mi nevysvětlíš postup už jsem pochopil, zkus mi teda alespoň zadat tvé otázky jednoznačně.
A zkus mi, prosím, dát jednoznačnou odpověď na tuto otázku: Jestliže se umím rozhodnout o výrazu $(-1)^{n}$ (jinými slovy (tvými) tento výraz JE definovaný), proč limita $\lim_{n \to \infty }\frac{1+(-1)^{n}}{2}$ definovaná není?
Opakuji, posloupnosti jsme nějak zvlášť nedělali. A pokud jde o mojí zkoušku, o tu si strach nedělej. Protože jsme, opakuji, posloupnosti nedělali, nejsou jejím obsahem. Co jsme dělali, převážně ovládám. Ovšem ve skriptech jsem přesto narazil na tyto limity a rád bych je pochopil. Proto si, prosím, přestaň utahovat z mé nechápavosti a zkus mi konstruktivně poradit. Děkuju.

vlado_bb · 07. 01. 2015 23:02

↑ jelinekgreen:Dement v ziadnom pripade nie si, len v tom zatial nemas jasno. Podme teda na to. Postupnost 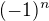$(-1)^n$ limitu nema, ukaze sa to lahko z definicie limity. V tvojej povodnej otazke pises v bode a o postupnosti $\{\frac{n+(-1)^{n}}{n-(-1)^{n}}\}_{n=1}^{\infty}$ . Ta limitu ma, co sa tiez pomerne lahko ukaze z definicie limity. Najprv ale musime odhadnut jej hodnotu. Preto nas zaujimaju jej cleny s velkym poradovym cislom. Dufam ze je to uz jasnejsie, ak nie, pokracovanie zajtra, teraz uz opustam pocitac.

kexholm · 07. 01. 2015 23:10

$\lim_{n \to \infty }\frac{n+(-1)^{n}}{n-(-1)^{n}}$

Proč by to nemělo mít limitu? Představ si to takhle, pro sudé n:

$\lim_{n \to \infty }\frac{n+1}{n-1}$

Pro liché n se to přehodí. Připomínám $(-1)^n \text{ kdy n je sudé} = 1$

$\lim_{n \to \infty }\frac{n-1}{n+1}$

Autor skryl část textu. Zobrazit/skrýt!

vlado_bb · 08. 01. 2015 08:59

↑ kexholm:Kexholm, to je v uplnom poriadku, ale mam zle skusenosti, ze vlastnost, ktoru si pouzila, si zaciatocnici dokazu pretransformovat takto: Ak v postupnosti najdem NEJAKE dve podpostupnosti s rovnakou limitou, tak aj povodna postupnost je konvergentna s tou istou limitou. Preto som sa radsej tymto smerom neuberal. Ak si prejdes diskusiu, zistis, ze zadavatel otazky zrejme zatial nie prilis dokladne chape, co vlastne konvergencia znamena, ale zato sa pridrziava (vedome alebo intuitivne) pravidla $\lim \frac{a_n+b_n}{c_n+d_n}=\frac{\lim a_n+\lim b_n}{\lim c_n + \lim d_n}$ bez akychkolvek existencnych predpokladov, co potom vedie k uzaverom, ake mozes sledovat v diskusii. Preto je podla mna nevyhnutnym prvym krokom samotny pojem limity (co zasa vyzaduje mat aku taku predstavu o postupnosti, s ktorou pracujeme - preto som bol taky otravny s tym tisicim clenom). Ale aj po zvladnuti definicie limity by som ho smeroval pri ulohe tohoto druhu skor k vetam typu $a_n \le b_n \le c_n$ ako na zradnu podu podpostupnosti :) V kazdom pripade ale ocenujem, ze sa veci snazi porozumiet a nie je to ocividne clovek typu "sem s vysledkom a to hned".

jelinekgreen

↑ vlado_bb: Tak v prvé řadě se chci omluvit za nevhodný tón posledního příspěvku. Už jsem byl večer trochu podrážden z toho, že to nechápu..
Přečetl jsem si znovu nějakou teorii a přiznávám se, že mě to nezachránilo. Aby limita existovala, musí splňovat nějaké věty a jelikož nevím, jak si ukázat, že limity 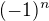$(-1)^n$ a $\lim_{n \to \infty }\frac{n+(-1)^{n}}{n-(-1)^{n}}$ existují, zřejmě jim úplně nerozumím. Jestli to hledat na základě kritérií konvergence nebo v jiných větách. Proč limita $\lim_{n \to \infty }\frac{1+(-1)^{n}}{2}$ neexistuje, tuším, souvisí s tím, že vychází různé výsledky, ale opět se neumím rozhodnout podle které věty si to dokázat.

Nicméně, jakmile jsem připustil fakt, že první neexistuje, ale druhá ano - její výsledek jsem pochopil. Zkrátka čitatel se bude od jmenovatele lišit o stále menší procento a tak se zlomek blíží jedné.

V případě $\lim_{n \to \infty }\frac{(-1)^{n}}{n}$ je úvaha obdobná. -1 nebo +1 je děleno stále vyšším číslem a zlomek tak konverguje v obou případech k nule. Tedy $\lim_{n \to \infty }\frac{(-1)^{n}}{n}=0$

V posledním případě ale pořád tápu: $\lim_{n \to \infty }\frac{(n)^{n}}{n!}$

Pokud dosadím, dostanu se na tvar 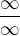$\frac{\infty }{\infty }$ A to mi naznačuje L´Hospitala. Ale jak zderivovat faktoriál nevím a na internetu jsem vykoumal, že výsledkem je matika daleko za hranicemi kurzu. Takže nejspíš nějaká úprava, úvaha, ale nevím, kde začít. Intuitivně očekávám, že v čitateli bude "větší" nekonečno a výsledek bych řekl, že bude tedy nekonečno. Ale rád bych více než intuici.

Pavel · 08. 01. 2015 13:57 — Editoval Pavel (08. 01. 2015 13:58)

↑ jelinekgreen:

K výpočtu limity

$\lim_{n \to \infty }\frac{(n)^{n}}{n!}$

můžeš použít tzv. Stirlingův vzorec

Nebo lze limitu určit použitím vhodných odhadů - nejlépe nerovností mezi aritmetickým a geometrickým průměrem. Záleží na tom, jaké techniky můžeš použít.

---

Existence limity

$\lim_{n \to \infty }\frac{n+(-1)^{n}}{n-(-1)^{n}}$

plyne z následujících odhadů:

$n-1\leq n+(-1)^n\leq n+1,\qquad n-1\leq n-(-1)^n\leq n+1$

Proto zřejmě platí

$\frac{n-1}{n+1}\leq\frac{n+(-1)^n}{n-(-1)^n}\leq\frac{n+1}{n-1}$

Teď stačí použit větu o limitě "sevřené" posloupnosti.

vlado_bb

↑ jelinekgreen:Ahoj, to je uplne v poriadku, ide o limity a nie o nejaky ton. Rozdelim svoju odpoved do dvoch casti. V tejto prvej sa pozrime na $\lim_{n \to \infty}(-1)^n$ . Moze tato limita byt 1? Ak by to tak bolo, ku kazdemu okoliu cisla 1, teda napriklad k intervalu $(0.9; 1.1)$ by musel existovat taky clen postupnosti, ze vsetky za nim su uz v tomto okoli. Ale taky existovat nemoze, lebo ak by existoval a bol by to $k$ -ty clen, staci len vziat lubovolne neparne $m \ge k$ (a take celkom iste existuje) no a uz vidime, ze $m$ -ty clen postupnosti bude $-1$ co ale nie je prvok intervalu $0.9;1.1)$ . Uplne rovnako sa ukaze ze ani $-1$ limitou byt nemoze.
Ak by chcelo byt limitou cislo $a$ ine ako $1$ alebo $-1$ , tak vezmeme take jeho okolie, ze v nom nebude ani $1$ ani $-1$ . Ak by malo byt toto $a$ limitou, od isteho indexu (poradoveho cisla clena postupnosti) by v nom musel byt uz kazdy clen tejto postupnosti. Ale v takomto okoli nie je ani jeden.

Hotovo. Bolo ti jasne vsetko? Kazde jedno slovo? Je dolezite, aby si toto vsetko presne pochopil.

Pokracovanie o chvilku. Bez Stirlingovho vzorca.

vlado_bb

↑ vlado_bb:Pokusim sa vysporiadat s $\lim_{n \to \infty} \frac{n^n}{n!}$ s minimalnou matematikou v pozadi. Nieco ale predsa len musim predpokladat ze vies, konkretne dve veci. Tou prvou je takato vlastnost postupnosti: Ak pre kazde $n \in N$ je $a_n \le b_n$ , pricom $\lim_{n \to \infty} a_n = \infty$ , tak aj $\lim_{n \to \infty} b_n = \infty$ . Rozumies tomuto tvrdeniu? Vies si to ak aj nie dokazat, tak aspon predstavit, pripadne nakreslit?

Ta druha vec je dokaz matematickou indukciou. Poznas tento typ dokazu?

Ak odpovies na obidve veci kladne, ideme dalej, ak nie, mozem vysvetlit jednu alebo obidve podrobnejsie. Ozvi sa.

jelinekgreen · 08. 01. 2015 14:19

↑ vlado_bb: První příspěvek jsem pochopil. Po třetím pročtení. To je tedy ta Bolzanova-Cauchyova podmínka, že? Na to jsem včera koukal poměrně nechápavě. Po tvém příspěvku už je to jasné. Teď jde na ten druhý.

Jo, to se zdá jasné. Zhruba řečeno, roste-li jedna posloupnost a druhá nemá n-tý člen menší - roste taky.
Matematickou indukci znám, nemůžu ovšem tvrdit, že bych pomocí ní, nalézal důkazy snadno. Ale princip je mi jasný.

vlado_bb

↑ jelinekgreen:Tak podme na to. Ukazeme najprv (indukciou), ze pre kazde $n \in N$ je $n! \le n^{n-1}$ .

Prvy krok: ak 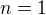$n=1$ , tak $n! = 1! = 1 \le 1 = 1^0 = n^{n-1}$
(mozno trochu zbytocne rozvlacne, ale snad nevadi).

Druhy krok: Predpokladame, ze $n! \le n^{n-1}$ , chceme ukazat ze $(n+1)! \le (n+1)^n$ .

Zacneme upravovat lavu stranu nerovnosti, ktoru chceme dokazat.

$(n+1)! = n! (n+1) \le$ (teraz vyuzivame to, co predpokladame) $\le n^{n-1}(n+1) \le (n+1)^{n-1}(n+1)=(n+1)^n$ .

Tym sme nerovnost $n! \le n^{n-1}$ dokazali.

Zvysok je uz lahky. Staci si vsimnut ze $\frac{n^n}{n!} \ge \frac {n^n}{n^{n-1}}=n$ , kde sme pri nerovnosti vyuzili prave dokazanu nerovnost.

No a nakolko $\lim_{n \to \infty}n = \infty$ , je aj $\lim_{n \to \infty} \frac{n^n}{n!} = \infty$ .

Matematické Fórum

#1 07. 01. 2015 21:42

Nevlastní limita

#2 07. 01. 2015 21:43

Re: Nevlastní limita

#3 07. 01. 2015 21:44

Re: Nevlastní limita

#4 07. 01. 2015 21:53

Re: Nevlastní limita

#5 07. 01. 2015 21:54

Re: Nevlastní limita

#6 07. 01. 2015 21:56

Re: Nevlastní limita

#7 07. 01. 2015 21:57

Re: Nevlastní limita

#8 07. 01. 2015 22:05

Re: Nevlastní limita

#9 07. 01. 2015 22:07

Re: Nevlastní limita

#10 07. 01. 2015 22:09

Re: Nevlastní limita

#11 07. 01. 2015 22:13 — Editoval vlado_bb (07. 01. 2015 22:14)

Re: Nevlastní limita

#12 07. 01. 2015 22:16

Re: Nevlastní limita

#13 07. 01. 2015 22:27

Re: Nevlastní limita

#14 07. 01. 2015 22:30

Re: Nevlastní limita

#15 07. 01. 2015 22:42

Re: Nevlastní limita

#16 07. 01. 2015 22:54

Re: Nevlastní limita

#17 07. 01. 2015 23:02

Re: Nevlastní limita

#18 07. 01. 2015 23:10

Re: Nevlastní limita

#19 08. 01. 2015 08:59

Re: Nevlastní limita

#20 08. 01. 2015 13:37 — Editoval jelinekgreen (08. 01. 2015 13:41)

Re: Nevlastní limita

#21 08. 01. 2015 13:57 — Editoval Pavel (08. 01. 2015 13:58)

Re: Nevlastní limita

#22 08. 01. 2015 14:02 — Editoval vlado_bb (08. 01. 2015 14:03)

Re: Nevlastní limita

#23 08. 01. 2015 14:08 — Editoval vlado_bb (08. 01. 2015 14:09)

Re: Nevlastní limita

#24 08. 01. 2015 14:19

Re: Nevlastní limita

#25 08. 01. 2015 14:33 — Editoval vlado_bb (08. 01. 2015 14:35)

Re: Nevlastní limita

Zápatí