Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 13. 01. 2015 11:47
#5 13. 01. 2015 12:40
#8 13. 01. 2015 14:36 — Editoval vulkan66 (13. 01. 2015 14:38)
- vulkan66


- Místo: Praha
- Příspěvky: 416
- Škola: ČVUT FJFI - Částicová fyzika
- Pozice: student
- Reputace: 20
Re: zahadna limita
↑ fyzika:
Omlouvám se, že ještě otravuju, ale v té poslední limitě pořád vzniká neurčitý výraz, takže nelze udělat limitní přechod. Správně je to takto: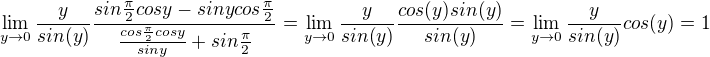
Vím, jak ovládat vesmír. Tak mi řekněte, proč bych se měl hnát za milionem? -Grigorij Perelman
Offline
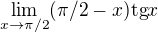
 . Úloha se tím změní na výpočet
. Úloha se tím změní na výpočet  ,
, takto? Nic mudrejsie ma nenapada
takto? Nic mudrejsie ma nenapada ,
,  ze zlomku
ze zlomku  víme (nebo ověříme pomocí L'H.), že je 1.
víme (nebo ověříme pomocí L'H.), že je 1.
 konkretní hodnoty (0 resp 1),
konkretní hodnoty (0 resp 1),