Matematické Fórum

Callme · 15. 01. 2015 00:58 — Editoval Callme (15. 01. 2015 01:13)

Dobry den,
Ako vyriesim $\int_{}^{}sin(6x)cos(8x)dx$ bez toho aby som pouzil tento vzorec ?

Pavel · 15. 01. 2015 07:34

↑ Callme:

Zkus per partes.

Freedy · 15. 01. 2015 07:35

↑ Callme:
Ahoj, jaké vzorce smíš a jaké nesmíš použít?

Callme · 15. 01. 2015 11:53 — Editoval Callme (15. 01. 2015 11:54)

↑ Freedy:
Mozem Odkaz

jelena · 15. 01. 2015 13:05

Zdravím,

↑ Callme: pokud zatím předpokládáš použití tabulkových vzorců pro integrování (ne další techniky integrování), potom můžeš uvažovat každou vhodnou a povolenou úpravu zápisu funkce - tedy úpravy algebraických výrazů, použití goniometrických vzorců apod. Proto bych zrovna upřednostnila použití goniometrických vzorců před integrováním, jelikož tak se pohodlně dostaneš ke vzorcům 4. řádku tabulky.

Byl nějaký důvod, že jsi hledal jinou metodu, než goniometrické úpravy? Děkuji.

Callme · 15. 01. 2015 15:49

Ktory goniometricky vzorec mam pouzit?

Jj · 15. 01. 2015 16:00

Dobrý den.

Řekl bych, že ten, který jste si tady ↑ Callme: zakázal.

Freedy · 15. 01. 2015 16:23

Ahoj,

a nebo si například odvodit $\cos 8x$ a $\sin 6x$ , jako:
$\cos 8x=\sin ^8x+\cos ^8x-28\sin ^2x\cos ^6x+70\sin ^4x\cos ^4x-28\sin ^6x\cos ^2x$
$\sin 6x=6\sin x\cos ^5x-20\sin ^3x\cos ^3x+6\sin ^5x\cos x$ , vypočítat:
$\sin 6x\cdot\cos 8x$ a nakonec rozdělit výsledný integrál na součet integrálů. Poté budeš již používat jednoduché substituce, či identity typu. Tento postup považuji za nejhorší

jelena · 15. 01. 2015 16:40

Zdravím v tématu,
↑ Jj: děkuji, ano - měla jsem na mysli vzorec, který v odkazu je označen jako "Součiny goniometrických funkcí".

Nejvíce by prospělo znát důvod nepoužitelnosti vzorce z příspěvku ↑ č. 1:: Od toho lze odvozovat další možné návrhy.

Pavel · 15. 01. 2015 17:33

↑ Freedy:

Metoda per partes je zakázána? Výpočet by byl na dva řádky. Použitím vzorců se nakonec nevyhneš substitucím, což je dle mého názoru náročnější technika než per partes.

Callme · 15. 01. 2015 18:48

↑ jelena: Neviem preco ale ten vzorec nemozeme pouzivat

misaH · 15. 01. 2015 18:54

↑ Callme:

A prečo nereaguješ na per partes?

Veď to je ideálne.

Možno preto vám nechcú dovoliť tú úpravu goniofunkcií - aby ste sa pocvičili v pp.

jelena · 15. 01. 2015 21:03

↑ Callme:

děkuji. Pokud jsi pořád u stejných materiálů, jak jsi mi dával odkaz, tak potom u vás ho učitel zařazuje jako vzorový do per partes (str. 45) - v takovým postupem není problém a to už používat můžete? viz kolega ↑ Pavel:

OT: ↑ Freedy: zkus raději použit exponenciální tvary sin(az) a cos(bz) pro komplexní obor (je to sice "umělý" krok, ale účinný (nejlépe přidáním editu do ↑ Freedy: - téma je přeci jen kolegy a bylo by dobré, kdyby se v problému (a hlavně ve formulaci problému) konečně zorientoval). Děkuji a zdary.

Freedy · 15. 01. 2015 23:22

↑ jelena:
Ahoj, já jsem to spíš bral tak, že hrubou silou, lze přece vždy dosáhnout kýženého výsledku.
Samozřejmě bych tento postup nikdy nevyužil, ledaže by to byla nějaká hnusná funkce, pro kterou by neexistoval vzorec.
Přijde mi, že je ale dost "hnusné" nepoužívat některé vzorce a některé ano. Když si některé vzorce odvodit umím, tak je přeci použít můžu. Chápu, že třeba používání L'hospitalova pravidla při výpočtu limit může být někdy zakázáno kvůli nepoužívání derivací. Ale derivace je přeci speciální typ limity, tak proč jej nepoužít? Nechápu.
Zpět k tématu, nejspíš už nemám žádný zájem vyjadřovat se k tématům, kde se něco zakazuje. Tak buď použijeme libovolný vzorec a nebo žádný. S možnosti, že "toto nepoužijeme" radši ani nebudu kalkulovat, ani teď, ani v budoucnu. A až mi někdo napíše, že nemůžu něco použít, tak si to tam přeci můžu odvodit prostředky, které použít můžu a tím dokázat, že použitý prostředek je platný a tudíž použitelný.

Mimochodem, vzorec na součet sinu a kosinu není zrovna extra těžký.

jelena · 15. 01. 2015 23:48

↑ Freedy:

také pozdrav.

že hrubou silou, lze přece vždy dosáhnout kýženého výsledku.

kéž by, to bych tu hrubou sílu použila hned :-)

Zpět k tématu, nejspíš už nemám žádný zájem vyjadřovat se k tématům, kde se něco zakazuje.

To je spíš problém, jak je formulován úvodní příspěvek tématu - jasné odůvodnění, proč jedná (nebo více) metod nemohou být použity, mi přijde rozumné a srozumitelné, co dál. Může tak být postavena metodika učitele, tak proč ne? Jen to kolega má napsat jasně - ne, že to 14 příspěvků řešíme.

Máme sekci "Metodiky-didaktiky", kde případně můžeš rozebrat Tvůj pohled ↑ Freedy:, v tomto tématu zůstaňme, prosím, u tématu ↑ Callme:. Děkuji.

misaH · 16. 01. 2015 06:11 — Editoval misaH (16. 01. 2015 06:47)

Kolega ako študent nemusí vedieť, prečo sa niečo zakazuje. Napísal jasne, že goniovzorec nie.

↑ Freedy:

Autor skryl část textu. Zobrazit/skrýt!

...

Freedy · 16. 01. 2015 08:37 — Editoval Freedy (16. 01. 2015 08:37)

↑ misaH:
Ahoj, já per partes neignoruji, jen si myslím, že věta o integrování per-partes a následná věta o substituci jsou určitě těžší poznatky než tento gon. vzorec. Chápu, že na procvičování per-partes se tado metoda zakázat může.
Integrování nuceným způsobem mi přijde hloupé z toho hlediska, že se pak studenti můžou vázat na tento postup a pak je někdy ani nenapadne, že se použitím gon. vzorců můžou k výsledku dostat 3x rychlejší cestou.
A přijde mi, že člověk se nenaučí per-partes integraci tím, že bude počítat tisíce příkladů na per-partes. Stačí ji pochopit.

Jen tak otázka, mimo téma, pro ↑ misaH: ↑ jelena:.
Pokud je věta o substituci založená na derivaci složené funkce a metoda per-partes na derivaci součinu dvou funkcí, tak je nějaká věta o integrování, která je založená na derivaci podílu dvou funkcí?

Pavel · 16. 01. 2015 09:44 — Editoval Pavel (16. 01. 2015 09:44)

↑ Freedy:

podíl dvou funkcí se převádí na součin, takže opět per partes nebo substituce. Stručně řečeno, pokud nepoužiješ zakázaný vzorec z prvního příspěvku, per partes nebo substituci, tak zadaný integrál nespočítáš.

Buď budeš mít v argumentu zadaných funkcí násobky proměnné x, tj. 6x nebo 8x, a pak musíš použít substituci, nebo ty funkce rozepíšeš pomocí součtových vzorců a vzniknou ti tak součiny goniometrických funkcí. Ty bez použití per partes nebo substituce nezintegruješ.

jelena · 16. 01. 2015 10:53 — Editoval jelena (16. 01. 2015 10:56)

Zdravím,

k ↑ příspěvku 1: pokud se vyloučí použití jednoho vzorce, tak to ještě neznamená, že bude jednoznačně zadána jiná metoda. Naopak: lze tvrdit, že každá jiná je vhodná (tu u nás již po druhé uzavřeli Náměstí, přes které standardizovaně chodím, no těch mých úvah - kam teď :-). Přesné zadání neznáme. Pokud znělo: vyřešte tuto úlohu použitím 2 různých metod, tak už je to alespoň nějaké vodítko. V jiných tématech kolegy je obdobná formulace "přes diferenciální počet bez použití analytické geometrie" (opravdu se to dá striktně dodržet? :-)).

Pavel napsal(a):
násobky proměnné x, tj. 6x nebo 8x,

ve vzorcích tuto "drobnou" (lineární) substituci obchází - viz tabulkové vzorce ↑ příspěvek 5:.

Abych tu jen tak netlachala:

- použití goniometrického vzorce ↑ příspěvek 1: je jasné, je na tři "=".
- per partes přímo od učitele kolegy,
- kolega ↑ Freedy: + mé vylepšení: nahradím 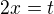$2x=t$ , potom $\frac{1}{2}\int \cos 4t\sin 3t\d t$ ,
- můj návrh $\int \frac{e^{i 6x} - e^{-i 6x}}{2i}\cdot \frac{e^{i8x}+e^{-i8x}}{2}\d x$ ,
- PR řádek: použití MAW.

Děkuji za další návrhy.

Matematické Fórum

#1 15. 01. 2015 00:58 — Editoval Callme (15. 01. 2015 01:13)

Integrál

#2 15. 01. 2015 07:34

Re: Integrál

#3 15. 01. 2015 07:35

Re: Integrál

#4 15. 01. 2015 11:53 — Editoval Callme (15. 01. 2015 11:54)

Re: Integrál

#5 15. 01. 2015 13:05

Re: Integrál

#6 15. 01. 2015 15:49

Re: Integrál

#7 15. 01. 2015 16:00

Re: Integrál

#8 15. 01. 2015 16:23

Re: Integrál

#9 15. 01. 2015 16:40

Re: Integrál

#10 15. 01. 2015 17:33

Re: Integrál

#11 15. 01. 2015 18:48

Re: Integrál

#12 15. 01. 2015 18:54

Re: Integrál

#13 15. 01. 2015 21:03

Re: Integrál

#14 15. 01. 2015 23:22

Re: Integrál

#15 15. 01. 2015 23:48

Re: Integrál

#16 16. 01. 2015 06:11 — Editoval misaH (16. 01. 2015 06:47)

Re: Integrál

#17 16. 01. 2015 08:37 — Editoval Freedy (16. 01. 2015 08:37)

Re: Integrál

#18 16. 01. 2015 09:44 — Editoval Pavel (16. 01. 2015 09:44)

Re: Integrál

#19 16. 01. 2015 10:53 — Editoval jelena (16. 01. 2015 10:56)

Re: Integrál

Pavel napsal(a):

Zápatí