Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Reziduum komplexní funkce (TOTO TÉMA JE VYŘEŠENÉ)
#1 19. 01. 2015 17:38
Reziduum komplexní funkce
Dobrý večer
Potřeboval bych nakopnout a najít, co dělám špatně. Mám najít rezidua fce  v jejich izolovaných singulárních bodech.
v jejich izolovaných singulárních bodech.
Po úpravě dostanu  . Z toho vidím, že jsou 3 nulové body.
. Z toho vidím, že jsou 3 nulové body.
0 - pól 3. řádu
-2 - jednoduchý pól
+2 - jednoduchý pól
V bodech 0 a -2 rezidua spočítám, problém mi dělá bod +2. Postup jsem si kontroloval podle přednášek i podle Rektoryse. Postupuju zhruba takto:
Ovšem podle výsledků ostatních reziduí i podle Wolframu má vyjít  .
.
Kde dělám chybu?
Radim, tedy jsem.
Dobrá rada je drahá, ta moje je zdarma.
Offline
- (téma jako vyřešené označil(a) rleg)
#2 19. 01. 2015 18:13 — Editoval Bati (19. 01. 2015 18:16)
Re: Reziduum komplexní funkce
Ahoj ↑ rleg:
neměl bys to spíš násobit výrazem  ? (viz např. http://cs.wikipedia.org/wiki/Reziduum , výpočet reziduí)
? (viz např. http://cs.wikipedia.org/wiki/Reziduum , výpočet reziduí)
Obecně Laurentovy řady se středem v 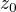 se píšou ve tvaru
se píšou ve tvaru  a ne
a ne  , protože by to tam akorát přidalo
, protože by to tam akorát přidalo 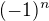 u
u  .
.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Reziduum komplexní funkce (TOTO TÉMA JE VYŘEŠENÉ)

