Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 17. 01. 2015 11:02
Re: maximum value
↑ stuart clark:![kopírovat do textarea $\mathrm{Dom}_f=\mathbb{R}\setminus\{\sqrt[3]{-1\pm\sqrt 2}\}$](/mathtex/11/11c05f91d87a9ed9b250ee47134ade00.gif) . Both numbers where the function f is not defined are less than 1, so f is a continous function for
. Both numbers where the function f is not defined are less than 1, so f is a continous function for  . Let us find the derivative of f:
. Let us find the derivative of f:
Let us denote  . Then the complex numbers
. Then the complex numbers 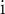 and
and  are roots of
are roots of 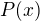 , therefore
, therefore 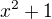 divides
divides 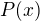 and
and 
The equation  is an algebraic reciprocal equation. Let us divide it by
is an algebraic reciprocal equation. Let us divide it by 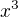 and modify it in the following way:
and modify it in the following way:
The equation has only two real roots:  and
and 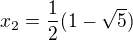 . Therefore
. Therefore  is divisible by
is divisible by  and
and
moreover  has no real roots and
has no real roots and  for
for  .
.
Using the previous results we can express the derivative f' in the following way:
If  then there is only one stationary point,
then there is only one stationary point, 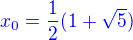 . Since
. Since 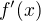 is positive on
is positive on  and negative on
and negative on  , the point
, the point  is a global maximum of
is a global maximum of  on
on  . Finally,
. Finally,
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#3 22. 01. 2015 09:28
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Re: maximum value
↑ Pavel: Thanku pavel for Nice explanation.
My Solution ::
Given  Where
Where 
So We can Simplify 
Now Let 
So ![kopírovat do textarea $\displaystyle f(u) = \frac{u}{u^3+3u+2}=\frac{u}{u^3+u+u+u+1+1}\leq \frac{u}{6\sqrt[6]{u^3\cdot u \cdot \cdot u \cdot u\cdot 1\cdot 1}} = \frac{1}{6}$](/mathtex/ab/ab3a14154bf283b8124fc25e092d89e1.gif)
Using  and above equality hold when
and above equality hold when 
Offline
#4 22. 01. 2015 09:57
Re: maximum value
↑ stuart clark:
Nice solution. I suspected that mean inequalities were an appropriate tool to solve the problem. However, I did not find the right modification of the fraction.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
 Where
Where