Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 21. 01. 2015 20:10
Soucet rady
Zdravim,
narazil jsem na youtube na kratke video, kde autor mluvi o sume rady 1+2+4+8+... (asi neco jako sum(2^n)[0,nekonecno]). Cele je to nakonec v trochu jinem kontextu v dalsim videu. Jen by mne zajimalo, v komentarich spousta lidi rika, ze to co autor dela je spatne, ale nenasel jsem tam nikde nic moc presvedciveho proc.
Jen by mne zajimalo, jestli by mi neco takoveho mohl nekdo vysvetlit - spolu s dalsim videem rozumim proc predvadi sumaci, tak jak ji dela, nerozumim tomu, jak by to melo byt matematicky spravne?
Rovnou dopredu i podekuji za pripadne osvetleni :-).
Offline
#3 21. 01. 2015 20:26
Re: Soucet rady
Řekl bych, že je problém v tom odečtení. On tu řadu přerovnává, ale taková operace je (tuším) povolená jen u (absolutně?) konvergentních řad. Jak to udělat správně? Vypočítat částečný součet s_n a svézt n-ko limitou až do nekonečna. :-)
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#5 22. 01. 2015 11:45
Re: Soucet rady
↑ pietro:
Touhle casti jsem si nebyl mos jisty, kdyz jde ta rada do nekonecna, muzu se s tim takhle zastavit?
↑ vlado_bb:
Ok, diky.
↑ byk7:
Je to tak dramaticky rozdil, myslel jsem, ze odecist a secist to nakonec muzes jak chces, 3+2-1 (tady take nezalezi na poradi, co sectu drive)?
V kazdem pripade take diky, zkusim se po tom podivat dale :-).
Offline
#6 22. 01. 2015 11:51 — Editoval vlado_bb (22. 01. 2015 11:56)
Re: Soucet rady
O.o napsal(a):
↑ pietro:
Je to tak dramaticky rozdil, myslel jsem, ze odecist a secist to nakonec muzes jak chces, 3+2-1 (tady take nezalezi na poradi, co sectu drive)?
To, co plati pre konecne mnoziny, sa neda vzdy preniest na nekonecne. Skus napriklad v nekonecnom rade
dat najprv zatvorky takto
a potom takto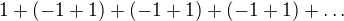 .
.
A ako bonbonik si pozri Riemannovu vetu o preusporiadani. Skratene hovori o tomto: Majme nejaky relativne konvergentny nekonecny rad. Napriklad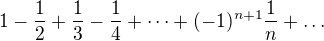 .
.
Vezmime si lubovolne realne cislo, napriklad 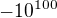 . Cleny uvedeneho radu sa daju poprehadzovat tak, aby po tom poprehadzovani bol sucet radu
. Cleny uvedeneho radu sa daju poprehadzovat tak, aby po tom poprehadzovani bol sucet radu 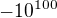 .
.
Offline
