Matematické Fórum

juraj1 · 23. 01. 2015 16:46

Zdravím,

počítám vlastní čísla z této matice: //forum.matweb.cz/upload3/img/2015-01/27649_maticeA.png

a zasekl jsem se na výpočtu determinantu s přidáním lamda:

jak z této rovnice vypočítám $\lambda$ 1,2,3 ?
(12- $\lambda$ )(6- $\lambda$ )(6- $\lambda$ )+172+72-[64(6- $\lambda$ )+99(12- $\lambda$ )+2(6- $\lambda$ )]

prosím o vysvětlení na tomto příkladu a nějaký obecný postup výpočtu pro tyto rovnice.

Děkuji

Jj · 23. 01. 2015 18:06

↑ juraj1:

Dobrý den. Pokud jsem se nepřepsal, tak charakteristická rovnice má tvar (x místo lambda):

$x^3-24 x^2+15 x+904=0$

V obecném případě je řešení docela problém. Absolutní člen (904) je součinem všech kořenů. Možno zkusit, zda rovnice nemá některý "jednoduchý" kořen rozložením absolutního členu na součin celých čísel.

V tomto připadě 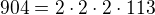$904 = 2\cdot 2 \cdot 2 \cdot 113$ a zkusit, zda některý ze součinů uvedených čísel není řešením (je třeba zkoušet kladné i záporné hodnoty). Řekl bych, že takto se dá "uhádnout" kořen x = 8.

Takže vydělit charakteristickou rovnici kořenovým činitelem (x-8), zbude kvadratická rovnice pro zbývající dva kořeny.

Pokud se takto nepodaří "uhádnout" některý jednoduchý kořen, tak asi některá z numerických metod řešení.

Eratosthenes

ahoj ↑ juraj1:,

v těchto školních příkladech bývají kořeny "malá celá čísla" a počítá se s použitím Hornerova schématu. Obvykle se začíná hádat +1, -1, což v tomto případě zjevně kořeny nejsou, a tak ta dvojka, na kterou přišel ↑ Jj:, je hned první rozumná volba...

o.neill · 23. 01. 2015 19:35

↑ Eratosthenes:
Zde bohužel právě dvojka kořen není, ale až ta osmička.

↑ juraj1:
Jenom ještě upozorním na chybku v původním příspěvku. Ten charakteristický polynom je
$(12-\lambda )(6-\lambda )(6-\lambda )+176+72-[64(6-\lambda )+99(12-\lambda )+2(6-\lambda )]$
a dá se upravit, na tvar, který už tu psal Jj. Tu rovnici pak je potřeba „nějak“ vyřešit, no. Tahle už je docela komplikovaná, takže nechce-li člověk použít nějaké odporné Cardanovy vzorce, musí kořen nějak uhodnout, jak psali kolegové.

juraj1 · 23. 01. 2015 21:11

Děkuji všem. Zkoušel jsem počítat jinou matici 3x3, kde jsem měl menší čísla a ta vyšla jednoduše jak říkáte. Kořen jsem uhádl, že je 1 a pak už se rovnice snadno dopočítala a vlastní čísla jsem našel.

Matematické Fórum

#1 23. 01. 2015 16:46

Hledám vlastní čísla matice 3x3

#2 23. 01. 2015 18:06

Re: Hledám vlastní čísla matice 3x3

#3 23. 01. 2015 19:25 — Editoval Eratosthenes (23. 01. 2015 19:26)

Re: Hledám vlastní čísla matice 3x3

#4 23. 01. 2015 19:35

Re: Hledám vlastní čísla matice 3x3

#5 23. 01. 2015 21:11

Re: Hledám vlastní čísla matice 3x3

Zápatí