Matematické Fórum

Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.

Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.

Nejste přihlášen(a). Přihlásit

Stránky: 1

 

#1 26. 01. 2015 19:04

Anonymystik
Příspěvky: 585
Reputace:   45 
 

Homogenní diferenciální rovnice s nekonstatntními koeficienty

Zdravím.
Prosím o pomoc s řešením této diferenciální rovnice:
$y \prime \prime + (A+B \delta(x))y = 0$,
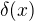kde $\delta(x)$ je Diracova delta funkce.
--
A ještě jeden související dotaz: jak se obecně dají řešit rovnice 2. řádu tvaru $y \prime \prime + f(x)y = 0$ ?

"Do you love your math more than me?"   "Of course not, dear - I love you much more."   "Then prove it!"   "OK... Let R be the set of all lovable objects..."

Offline

 

#2 26. 01. 2015 21:58

kafe_arabica
Příspěvky: 38
Reputace:   3 
 

Re: Homogenní diferenciální rovnice s nekonstatntními koeficienty

Ahoj.
Odpoveď je v Sturmovej - Liouvilleovej teórii a použití Greenovej funkcie.

Offline

 

 

Stránky: 1

Zápatí

Powered by PunBB
© Copyright 2002–2005 Rickard Andersson