Matematické Fórum

kafe_arabica · 25. 01. 2015 20:10

Ahoj.

Potreboval by som vysvetliť inklúziu týchto topológií. Niekde by normová a slabá mali aj splývať, myslím na jednotkovej guli v banachovom priestore a na konečnorozmerných v.p., ale nie som si istý.
A ešte celkom dôležitá vec. Kartézsky súčin je definovaný, http://en.wikipedia.org/wiki/Cartesian_ … e_products
Keby som to chcel "topologizovať", tak na súčine priestorov 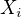$X_i$ vezmem súčinovú topológiu a čo ďalej? Na indexovej množine žiadnu a tie zobrazenia sú proste zobrazenia a nie sú nutne spojité?
Napríklad priestor $\mathbb{R}^\mathbb{R}$ , ak uvažujem topológiu na súčine. Potom prvky tohto pristoru sú funkcie (reálne funkcie reálnej premennej). Lenže na nich by mala byť topológia. Takže som z toho značne zmätený.
V tom prípade by som musel na indexovej množine brať topológiu a za prvky toho priestoru len spojité funkcie, no tým pádom som z kartézskeho súčinu vyhodil veľa prvkov.
Snáď je mi rozumieť, čomu nerozumiem :D.

kafe_arabica

A je topológia bodovej konvergencie jemnejšia ako slabá topológia?

K tomu $\mathbb{R}^\mathbb{R}$ . Keď už uvažujem topológiu, súčinovú, čo sú potom prvky $f\in \mathbb{R}^\mathbb{R}$ ? Sú to ľubovolné funkcie alebo spojité? Čo je potom okolie toho prvku? Je to okolie jeho funkčných hodnôť v $\mathbb{R}^\mathbb{R}$ v tej súčinovej topológii?

edit: Nejako mi nesedí okolie tej funkcie, to by mali byť tiež funkcie, nie hodnoty v obore hodnôt.

Brano · 26. 01. 2015 13:28 — Editoval Brano (26. 01. 2015 13:52)

inak mal by si trochu upresnit kontext o ktory sa zaujimas (t.j. ake presne priestory a tak) lebo bavit sa tak nejak vagne ta moze este viac dopliest.

+ este to ze som bol vcera ja nejaky dopleteny (cely ten komentar radsej skryjem aby nikoho neplietol)

tak este raz k tej bodovej a rovnomernej konvergencii.

rovnomerna konvergencia implikuje bodovu konvergenciu teda cim viac veci konverguje, tym menej prvkov ma topologia teda mnozinovo topologia bodovej je podmnozinou topologie rovnomernej

co sa tyka podmienok kedy sa zhoduju, tak zatial moju predchadzajucu (teraz uz skrytu) poznamku o spojitych fciach na kompakte neber vazne, este si to musim premysliet

dalej co sa tyka $R^R$ - trochu to zovseobecnime na $R^I$ kde $I$ je lubovolna indexova mnozina (na nej topologiu netreba)
cize $R^I$ je mnozina VSETKYCH funkcii z $I$ do $R$ a sucinova topologia ma SUBbazu okoli takehoto typu
$V_{x,\varepsilon}(f)=\{g\in R^I; |f(x)-g(x)|<\varepsilon\}$ (bazu tvoria vsetky mozne konecne prieniky)

no a co sa tyka topologie slabej konvergencia, tak na jej konstrukciu porebujes najprv spojity dual k $X$ cize musis upresnit aku topologiu na tom $X(=R^R?)$ mas z ktorej tu slabu konstruujes

kafe_arabica · 26. 01. 2015 14:47

Hovorme o $R^R$ . S tou subbázou súhlasím.
Nerozumiem ako sa definuje topológia bodovej konvergencie. Doteraz som mal za to, že to je práve tá súčinová topológia.
Ako súvisí topológia na X so slabou topológiou? Veď slabú konštruujem: Vezmem algebraický duál (lineárne zobrazenia z X do $R$ ), poprípade jeho podpriestor (kt, oddeľuje body) a požadujem, aby tieto zobrazenia boli spojité. Tým dostávam pseudonormy a lokálne konvexný X so slabou topológiou (generovanou pomocou pseudonoriem). Nikde sa tam nevyužíva pôvodná topológia.
No a malo by platiť, že slabá topológia je slabšia než silná (normová), čo by malo byť preto, lebo do slabého okolia sa dá vložiť normové okolie. Správne?

Brano · 26. 01. 2015 22:50 — Editoval Brano (26. 01. 2015 22:51)

aha - no ide o to ako tu slabu topologiu definujes - ja to poznam tak, ze mas X s topologiou, vezmes dual X* - to su vsetky SPOJITE linearne zobrazenia a vezmes najmensiu moznu topologiu na X, ze v nej budu stale vsetky prvky z X* spojite (takyto typ konstrukcie topologie sa vola aj inicialna topologia) a to co ti vznikne je slaba topologia a je slabsia ako ta povodna (silna)

ale samozrejme, ze mozes tu konstrukciu urobit aj s algebraickym dualom ale neviem ci bude vzdy zarucene, ze bude slabsia ako akakolvek normova topologia na X (ale mozno ze hej)

no a "slabsi" znamena ze ak nieco konverguje v "silnejsom" zmysle, tak to konverguje aj v "slabsom" a teda v slabsom moze konvergovat viac veci a teda "slabsia" je podmnozina "silnejsej"

a ano topologia bodovej konvergencie je presne ta sucinova az na taku jemnost, ze asi nazov topologia bodovej konvergencie by sa povedal iba v tom pripade ked su vsetky Xi rovnake - co je aktualne nas pripad
a co nieje jasne - to ze ta subbaza zodpoveda jej konstrukcii pomocou inicialnej topologie?

kafe_arabica · 26. 01. 2015 23:11

Ku konštrukcii slabej topológie. Poznám aj ten tvoj spôsob, len pomocou pseudonoriem môžeš dostať ešte slabšie topológie, lebo požaduješ, aby bolo menej lin. funkc. spojitých. To len tak, ak by sa ti to hodilo.

K inklúziám. Pomocou konvergencie to nevidím. Ak niečo konverguje "silno", tak to konverguje aj "slabo". T.j. množina postupností/sietí, ktoré konvergujú "slabo" je väčšia než tá druhá, prečo je inklúzia topológii opačná?

A odkiaľ vidím, že topológia bodovej konvergencie je slabšia než slabá topológia? Myslím z toho pohľadu konvergencie. Tam mi nie je hneď jasné, kde tých vecí konverguje viacej.

Brano · 27. 01. 2015 10:00 — Editoval Brano (27. 01. 2015 10:12)

uvedom si ako mas definovanu konvergenciu siete: pre vsetky U otvorene okolia plati bla bla - teda cim viac je tych U tak tym je ta podmienka restriktivnejsia a tym menej sieti konverguje: napr. v indiskretnej topologii (ci ako sa vola ta co ma iba dva prvky $\{\emptyset,X\}$ ) ti konverguju vsetky siete a v diskretnej topologii ( P(X) ) konverguju iba eventualne konstantne siete

a co sa tyka porovnania slabej (teraz tej tvojej) a sucinovej na $R^R$

slaba je inicialna zodpovedajuca systemu vsetkych linearnych zobrazeni z $R^R$ do $R$
a bodova je inicialna zodpovedajuca systemu vsetkych projekcii - lenze tie su linearne, teda ak nieco konverguje slabo, tak aj bodovo.

Matematické Fórum

#1 25. 01. 2015 20:10

slabá topológia, topológia bodovej konvergencie a normová topológia

#2 26. 01. 2015 00:36 Příspěvek uživatele Brano byl skryt uživatelem Brano. Důvod: zmatocne a vlastne aj nepravdive

#3 26. 01. 2015 00:43 — Editoval kafe_arabica (26. 01. 2015 00:45)

Re: slabá topológia, topológia bodovej konvergencie a normová topológia

#4 26. 01. 2015 13:28 — Editoval Brano (26. 01. 2015 13:52)

Re: slabá topológia, topológia bodovej konvergencie a normová topológia

#5 26. 01. 2015 14:47

Re: slabá topológia, topológia bodovej konvergencie a normová topológia

#6 26. 01. 2015 22:50 — Editoval Brano (26. 01. 2015 22:51)

Re: slabá topológia, topológia bodovej konvergencie a normová topológia

#7 26. 01. 2015 23:11

Re: slabá topológia, topológia bodovej konvergencie a normová topológia

#8 27. 01. 2015 10:00 — Editoval Brano (27. 01. 2015 10:12)

Re: slabá topológia, topológia bodovej konvergencie a normová topológia

Zápatí