Matematické Fórum

lukasstork · 27. 01. 2015 17:01

Ahoj potřeboval bych poradit, prej na tyhle priklady mame pouzit derivace funkci, ale ja vůbec nevim jak je mam pouzit. Diky za jakekoliv rady.

1) Do koule o poloměru r vepište rotační válec maximálního objemu.
2) Tvrdý papír tvaru obdélníku má rozměry 60 cm a 28 cm. V rozích se odstříhnou stejné čtverce a zbytek se ohne do tvaru otevřené krabice. Jak dlouhá musí být strana odstřižených čtverců, aby objem krabice byl největší ?

vulkan66

↑ lukasstork:

Ahoj, vzorec pro objem válce je $V=\pi r^{2}h$ . Ty potřebuješ funkci jen o jedné proměnné, takže si musíš vyjádřit $r$ pomocí poloměru koule $R$ (Pythagorova věta). Tu závislost dosadíš do funkce $V$ a zderivuješ podle výšky. Nakonec najdeš pro jakou výšku má funkce extrém.

lukasstork · 27. 01. 2015 18:06

↑ vulkan66: ahoj vyjádřil jsem si teda r z poloměru koule to je $\sqrt[3]{(V/(4:3)\pi }$ a potom to musím dosadit do toho objemu válce ?

vulkan66

↑ lukasstork:

Nene, tebe objem koule nezajímá. Pro tebe je poloměr koule konstanta, s tou nehýbeš. Možná jsem se špatně vyjádřil. Potřebuješ vyjádřit $r$ nějak pomocí poloměru koule $R$ . Představ si průřez středem koule s válcem uvnitř. Zkus tam najít pravoúhlý trojúhelník.

Edit:
Aby jsme si rozumněli, $r$ je poloměr podstavy válce a $R$ je poloměr koule.

lukasstork · 27. 01. 2015 18:24

r = R krát cosx je to dobře ?

vulkan66 · 27. 01. 2015 18:44

↑ lukasstork:

Ano, to je sice dobře, ale ještě by sis musel vyjádřit výšku. Podle mě je to takové složité a tak mám raději jiný postup.
Pomocí Pythagorovy věty: 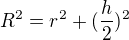$R^{2}=r^{2}+(\frac{h}{2})^{2}$ . Podívej se na obrázek a uvidíš to tam.
Do vzorce pro objem dosaď $r^{2}$ a zderivuj.

lukasstork · 27. 01. 2015 19:11

Takže to ma bejt $V=\pi\cdot v\cdot [R^{2}-\frac{h^{2}}{4}]$ a to stačí zderivovat a položit rovno 0

vulkan66 · 27. 01. 2015 19:15

↑ lukasstork:

Ano, ale pozor, že $v$ je to samé jako $h$ . Derivací najdeš extrém této funkce závislé pouze na výšce.

lukasstork · 28. 01. 2015 08:02

↑ vulkan66: a jak to pak bude prosím te na tom poloměru

Cheop · 28. 01. 2015 09:06 — Editoval Cheop (28. 01. 2015 09:08)

↑ lukasstork:
Objem válce je
$\pi r^2v$ kde r = poloměr válce, v = výška válce
Tento válec máme vepsat do koule o poloměru R tak,aby objem válce byl největší možný.
Dle obrázku
//forum.matweb.cz/upload3/img/2015-01/32059_vvk.png
$4R^2=4r^2+v^2\\v=\cdots\cdots$
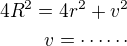
Objem válce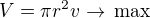
$V=\pi r^2v\rightarrow\,\text{max}$ - dosadíš výšku
Zderivuješ podle r a derivaci položíš rovnu 0
z toho určíš poloměr válce v závislosti na R
dopočítáš výšku válce v v závislosti na R a r
a nakonec maximální objem
Pokud budeš dobře počítat tak by ti mělo vyjít:

Autor skryl část textu. Zobrazit/skrýt!

Cheop · 28. 01. 2015 09:18 — Editoval Cheop (28. 01. 2015 10:25)

↑ lukasstork:
Př.2)
Označme:
strany obdélníku a,b
stranu čtverce x
Obrázek:
//forum.matweb.cz/upload3/img/2015-01/37124_krabic.png

Maximální objem bude: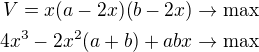
$V=x(a-2x)(b-2x)\rightarrow\text{max}\\4x^3-2x^2(a+b)+abx\rightarrow\text{max}$
Zderivovat podle x a derivaci položit rovnu 0
Vypočítat x a dosadit do výpočtu pro maximílní objem - toto obecně a pak s konkrétními zadanými hodnotami
Mělo by ti vyjít:

Autor skryl část textu. Zobrazit/skrýt!

Matematické Fórum

#1 27. 01. 2015 17:01

Slovní úlohy - extrémy

#2 27. 01. 2015 17:23 — Editoval vulkan66 (27. 01. 2015 17:23)

Re: Slovní úlohy - extrémy

#3 27. 01. 2015 18:06

Re: Slovní úlohy - extrémy

#4 27. 01. 2015 18:13 — Editoval vulkan66 (27. 01. 2015 18:20)

Re: Slovní úlohy - extrémy

#5 27. 01. 2015 18:24

Re: Slovní úlohy - extrémy

#6 27. 01. 2015 18:44

Re: Slovní úlohy - extrémy

#7 27. 01. 2015 19:11

Re: Slovní úlohy - extrémy

#8 27. 01. 2015 19:15

Re: Slovní úlohy - extrémy

#9 28. 01. 2015 08:02

Re: Slovní úlohy - extrémy

#10 28. 01. 2015 09:06 — Editoval Cheop (28. 01. 2015 09:08)

Re: Slovní úlohy - extrémy

#11 28. 01. 2015 09:18 — Editoval Cheop (28. 01. 2015 10:25)

Re: Slovní úlohy - extrémy

Zápatí