Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 31. 01. 2015 15:19
Funkcia s odmocninou
ahojte,
ak mam urcit obor hodnot tejto funkcie: y = 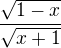
mozem postupovat tak, ze si urcim inverznu funkciu: y = 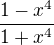
a teda definicny inverznej je vlastne obor hodnot povodnej...cize v tomto priprade je H(f) = R ?
Offline
- (téma jako vyřešené označil(a) Petra2014)
#2 31. 01. 2015 15:39
Re: Funkcia s odmocninou
↑ Petra2014:
Ahoj
Asi ťažko môže byť obor hodnôt  celá množina
celá množina  , keďže
, keďže  .
.
Technicky hľadáš všetky  , pre ktoré existuje
, pre ktoré existuje  také, že
také, že 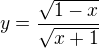
Z toho hneď  a za tej podmienky to môžeš umocniť, vyjadriť
a za tej podmienky to môžeš umocniť, vyjadriť  pomocou
pomocou  a potom ešte musíš zabezpečiť, aby pôvodné výrazy mali zmysel, tj. aby
a potom ešte musíš zabezpečiť, aby pôvodné výrazy mali zmysel, tj. aby 
1^6 - 2^6 + 3^6 = 666
Offline
#3 31. 01. 2015 15:40
Re: Funkcia s odmocninou
↑ Petra2014:Nieco nebude v poriadku, ak by bol definicny obor  , tak jednou z hodnot funkcie by bolo cislo -1, co nie je mozne.
, tak jednou z hodnot funkcie by bolo cislo -1, co nie je mozne.
Offline
#5 31. 01. 2015 15:47
Offline
#7 31. 01. 2015 16:16
Re: Funkcia s odmocninou
↑ Petra2014: je vypočítané v pohode
je vypočítané v pohode
Podmienka
by mala byť splnená potom pre každé  , takže jediná podmienka je
, takže jediná podmienka je 
1^6 - 2^6 + 3^6 = 666
Offline


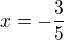 je
je 
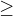 0, tak umocnim zadanu funkciu a dostanem
0, tak umocnim zadanu funkciu a dostanem  x = \frac{1-y^{2}}{1+ y^{2}}
x = \frac{1-y^{2}}{1+ y^{2}} \le 1
\le 1 >-1$
>-1$ )
) platí práve vtedy keď
platí práve vtedy keď platí práve vtedy keď
platí práve vtedy keď , čo platí vždy.
, čo platí vždy. platí práve vtedy keď
platí práve vtedy keď platí práve vtedy keď
platí práve vtedy keď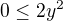 čo platí vždy
čo platí vždy