Matematické Fórum

maver · 01. 02. 2015 02:07

Dobrý den,

nerozumím, proč u následujících dvou příkladů byl použit odlišný postup.

Případ b) zde je $q=\frac{1}{2}$ a $q=\frac{1}{3}$ takže se nabízí limita částečného součtu (jako metoda výpočtu součtu řady) dle vzorce $sn=\frac{1}{1-q}$

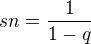
Případ c) se řeší pomocí limity "n" do nekonečna (čili ne jako v případě b)).

Je to tak?

//forum.matweb.cz/upload3/img/2015-02/52028_rady-konvergence.png

ttt_ · 01. 02. 2015 02:45 — Editoval ttt_ (01. 02. 2015 02:49)

v ulohe b) sa jedna o jednoduche geometricke rady...
v ulohe c) vidime takzvany teleskopicky rad (vid. Odkaz)
$s_n=\sum_{k=1}^{n}\frac{2k+1}{k^2(k+1)^2}=\sum_{k=1}^{n}\left[ \frac{1}{k^2}-\frac{1}{(k+1)^2}\right]=\\ =\frac{1}{1^2}-\frac{1}{2^2}+\frac{1}{2^2}-\frac{1}{3^2}+\frac{1}{3^2}-\ldots-\frac{1}{n^2}+\frac{1}{n^2}-\frac{1}{(n+1)^2}$
Okrem prveho a pesledneho clena vsetky cleny vypadnu..., a potom:
$\lim_{n\to\infty}s_n=\lim_{n\to\infty}\left(\frac{1}{1^2}-\frac{1}{(n+1)^2}\right)=1-0=1$

maver · 01. 02. 2015 14:26

↑ ttt_:
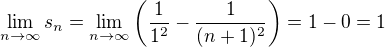
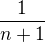prosím o vysvětlení, proč v posledním řádku jednou za n dosazujete 1 a hned v dalším $\frac{1}{n+1}$ řešíte tento zlomek klasicky jako limitu do nekonečna. Podle mého špatného chápání by i ten první 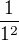$\frac{1}{1^{2}}$ měl být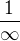 $\frac{1}{\infty }$

ttt_ · 01. 02. 2015 15:15 — Editoval ttt_ (01. 02. 2015 15:17)

↑ maver:
Sucet jednoducho rozpises..., len prvy a posledny clen nevypadnu, takto uz to vidiet?
$s_n=\sum_{k=1}^{n}\frac{2k+1}{k^2(k+1)^2}=\sum_{k=1}^{n}\left[ \frac{1}{k^2}-\frac{1}{(k+1)^2}\right]=\\ =\left( \frac{1}{1^2}-\frac{1}{(1+1)^2}\right) + \left( \frac{1}{2^2}-\frac{1}{(2+1)^2} \right) + \left(\frac{1}{3^2}-\frac{1}{(3+1)^2}\right)+\ldots \\ \ldots+\left(\frac{1}{(n-1)^2}-\frac{1}{((n-1)+1)^2}\right)+\left(\frac{1}{n^2}-\frac{1}{(n+1)^2}\right)=\\ =\frac{1}{1^2}-\frac{1}{2^2}+\frac{1}{2^2}-\frac{1}{3^2}+\frac{1}{3^2}-\frac{1}{4^2}\ldots+\frac{1}{(n-1)^2}-\frac{1}{n^2}+\frac{1}{n^2}-\frac{1}{(n+1)^2}=\\ =1 - \frac{1}{(n+1)^2}$

maver · 01. 02. 2015 16:17

↑ ttt_:
no, mám krátce před zkouškou, tak tohle už nestíhám pochopit.

Ale nyní rozumím tomu, že máme ve cvičeních zkrácenou verzi delšího výpočtu a za to děkuji.

Matematické Fórum

#1 01. 02. 2015 02:07

Nekonečné řady a konvergence

#2 01. 02. 2015 02:45 — Editoval ttt_ (01. 02. 2015 02:49)

Re: Nekonečné řady a konvergence

#3 01. 02. 2015 14:26

Re: Nekonečné řady a konvergence

#4 01. 02. 2015 15:15 — Editoval ttt_ (01. 02. 2015 15:17)

Re: Nekonečné řady a konvergence

#5 01. 02. 2015 16:17

Re: Nekonečné řady a konvergence

Zápatí