Matematické Fórum

found · 28. 01. 2015 13:54

Ahoj,

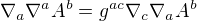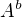snažím se spočítat si, jak vypadá výraz $\nabla_a\nabla^a A^b = g^{ac}\nabla_c\nabla_aA^b$ , kdy $A^b$ je nějaký obecný čtyřvektor na libovolné varietě - nemám žádnou speciální metrku z Einsteinových rovnic, potřebuji ten vzorec pro obecný prostoročas.

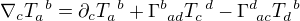Co jsem udělal, je definice $T_a^{~b} = \nabla_aA^b = \partial_aA^b + \Gamma^b_{~ac}A^c$ a poté $\nabla_cT_a^{~b} = \partial_cT_a^{~b} + \Gamma^b_{~ad}T_c^{~d} - \Gamma^d_{~ac}T_d^{~b}$ . Tím jsem se dostal k relativně složitému výrazu

$\nabla_c\nabla_aA^b = \partial_c(\partial_aA^b + \Gamma^b_{~ac}A^c) + \Gamma^b_{~ad}(\partial_cA^d + \Gamma^d_{~cd}A^d) - \Gamma^d_{~ac}(\partial_dA^b + \Gamma^b_{~de}A^e).$

Nevím ale, jak pokračovat dále, abych došel k nějakému hezčímu výrazu vyjádřenému pomocí obecné metriky. Mám na mysli výrazy typu kovariantní divergence
$\nabla_aA^a = \frac{1}{\sqrt{-g}}\partial_a\left(\sqrt{-g}A^a\right).$

Kdysi jsem viděl někde na internetu, že takový vzorec existuje i pro d'Alembertův operátor, ale nemůžu jej už nikde najít, tak se jej snažím odvodit.

S pozdravem a díky
Jimmy

Brzls · 30. 01. 2015 13:03 — Editoval Brzls (30. 01. 2015 17:32)

↑ found:

Čau

S odvozením asi nepomůžu, nicméně předpokládám že hledaný výsledek je zde (možná se pletu)
http://www.encyclopediaofmath.org/index … t_operator

Jelikož se jedná o poněkud pokročilejší problém, celé téma přesouvám do náročnějších, kde je větší šance že se ho ujme někdo povolanější

Edit:

Tak jsem na to koukal, a pokud se nepletu tak ono to vyplývá skoro přímo z toho vztahu pro divergenci
Dále bychom si ještě měli ujasnit jednu věc. Jsi si jistý, že potřebuješ působit tím operátorem na vektorovou funkci? Protože d´alembertián se většinou aplikuje na skalární funkce. Pokud to tak skutečně chceš, tak jediné co mě napadá je d´alembertiánem působit na koždou složku vektoru zvlášť, jestli je to možné to záleží na kontextu ve kterém to používáš.

Ale uvažujme nyní normální případ kdy f je nějaká skalární funkce a necháme na ní zapůsobit tím operátorem.
Jelikož f je skalární funkce, tak první kovariantní derivace je vlastně jen parciální, resp operátor čtyř-gradientu. Dále pak použijeme ten vzorec pro divergenci

$\nabla^{a}\nabla_{a}f=\nabla^{a}(\partial _{a}f)=\nabla^{a}(F_{a})=\nabla_{a}(F^{a})$
Písmeno F jsem akorát použil pro přehlednější zápis. JEden index se zvýšil a druhý snížil, což je v pořádku (to vyplývá z toho, že ta matice g s indexy nahoře je inverzní k té s indexy dole, je to sice kostrbatě řečeno ale snad je jasné proč to tak je, to nechci rozebírat)
dále již použijeme vlastnost divergence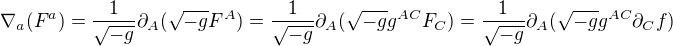
$\nabla_{a}(F^{a})=\frac{1}{\sqrt{-g}} \partial_{A}(\sqrt{-g}F^{A})=\frac{1}{\sqrt{-g}} \partial_{A}(\sqrt{-g}g^{AC}F_{C})=\frac{1}{\sqrt{-g}} \partial_{A}(\sqrt{-g}g^{AC} \partial_{C}f)$

Což je v souladu s tím vzorcem v tom odkazu. Co se týče odvození toho vztahu pro tu divergenci, tak to plyne přímo z definice, akorát je potřeba využít vztahu mezi Christoffelovými symboly a metrikou.
Doufám že tato odpověď je alespoň trochu přínosná. Kdyby ne tak upřesni jak to myslíš s tou aplikací d´alebertianu na ten čtyřvektor a nikoli skalár...

Jinak co se týče vlastností metriky a podobně tak jsem čerpal z tohoto zdroje http://www.aldebaran.cz/studium/otr.pdf je tam uveden právě i ten vztah mezi Christoffelovými symboly a metrikou.

found · 30. 01. 2015 19:20 — Editoval found (30. 01. 2015 20:04)

↑ Brzls:

Ahoj, děkuji, ten vzorec z odkazu je to, co jsem hledal.

On úplně z divergence jako takové asi nevychází, ne? Resp. v té divergenci se sčítá přes složku vektoru, jako jsi ukázal v postupu pod odkazem pro skalární funkci $f$ .

Možná se rovnou i zeptám, abych neřešil hloupost. Jde mi o vlnové Maxwellovy rovnice, tj. $\square A^b = 0$ , tj. řešení pro pole bez zdrojů, ale chci najít toto řešení v obecném prostoročase. Resp. o co se snažím je najít řešení Einsetinových rovnic pro elektromagnetické vlny. Nikam to nepotřebuji, jen mě začalo zajímat, jak by taková nestacionární a nestatická metrka vypadala.

Můj postup je ten, že hledám řešení vlnové rovnice pro 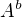$A^b$ , které chci poté dosadit skrze $F_{ab} = \nabla_aA_b - \nabla_bA_a$ do
$R_{ab} = 2\left(F_a^{~c}F_{bc} - \frac 14 g_{ab}F_{cd}F^{cd}\right) + \Lambda g_{ab},$
což je tvar Einsteinových rovnic pro elektromagnetické pole, alespoň se domnívám - 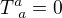$T^a_{~a} = 0$ a skalární křivost jsem nahradil závislostí na $\Lambda, T$ .

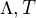Nebo existuje jiná cesta a jdu na to špatně? Vím, že už to není původní dotaz, tak se omlouvám, že takhle pokračuji, ale nemůžu si pomoct, jsem zvědavý. :-)

Edit: Co mě upřímně nejvíce mate je fakt, že samotné elektrické pole nějakým způsobem "křiví" prostoročas. Když tedy chci hledat vlny, nedejbože jejich zdroje, které by se pohybovaly, ovlivňují významným způsobem geometrii prostoročasu, jenže samotný prostoročas poté ovlivňuje jejich šíření, takže dokud nemám metriku, nemůžu vlastně tyto rovnice vůbec řešit, tudíž nevyřeším Einsteinovy?

S pozdravem
Jimmy

Brzls · 31. 01. 2015 11:27 — Editoval Brzls (31. 01. 2015 11:28)

↑ found:

Aha, tak ten odvozený vzorec je k ničemu, neboť vážně potřebujeme d´alembertian z vektorové funkce. NEvím jak se takovéhle rovnice řeší, nicméně místo pracování s čtyřpotenciálem bych možná radši zkusil pracovat přímo s tenzorem F. Tím pádem to vyjádření d´alembertianu ani nepotřebujeme, to ale neznamená že by to nějak nešlo.

Maxwellovy rovnice ve vakuu bez zdrojů v ohledem na křivost prostoru se dají zapsat jako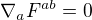

$\nabla_a F^{ab}=0$

Jenže pro tento vztah odvodíme vzorec podobný pro divergenci a zapíšeme tak Maxwellovy rovnice jako

$\frac{1}{\sqrt{-g}}\partial_a\left(\sqrt{-g}g^{ab}g^{cd}F_{bd}\right)=0$
(zdroj http://www.pas.rochester.edu/~rajeev/phy413/Grav12.pdf )

Jak si dospěl k tomu tvaru Einsteinových rovnic mi není úplně jasné (stejně tak jakou soustavu jednotek používáš vzhledem tomu že v té rovnici není žádná konstanta), ale to samozřejmě neznamená že to je špatně. Nicméně prostě stačí vzít Einsteinovy rovnice a stress-energy tenzor vyjádřit pomocí tenzoru F. To jak zbylé členy které určují zakřivení prostoru vyjádřit pomocí metriky to nevím, ale předpokládám že to jde.

Takže mám jednu sadu rovnic (Maxwellovy) a druhou sadu rovnic (Einsteinovy). Dohromady určují metriku a i vývoj elektromagnetického pole. Řešit je zvlášť podle mě nepůjde, ale jak řikám nemám tušení jak se takováhle sada rovnic řeší. Ale třeba je to blbost na to jít tak jak navrhuji. Určitě bych zkusil prohledat internet, divil bych se kdyby to někde nebylo podrobně prodiskutované.

found · 31. 01. 2015 14:24 — Editoval found (31. 01. 2015 14:29)

↑ Brzls:

Jsem zvyklý řešit z STR, případně klasické fyziky nejdříve potenciál, tak možná proto k tomu tak tíhnu. :-)

Díky za zdroj, to si pročtu. :-)

A taky díky za upozornění s konstantami. Uvažoval jsem $R = 4\Lambda - 8\pi T$ , takže po dosazení
$R_{ab} - \frac 12(4\Lambda - 8\pi T)g_{ab} + \Lambda g_{ab} = 8\pi T_{ab}.$

Potom jsem si vzal 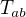$T_{ab}$ pro elektromagnetické pole 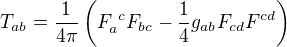$T_{ab} = \frac 1{4\pi}\left(F_a^{~c}F_{bc} - \frac 14 g_{ab} F_{cd}F^{cd}\right)$ . Po dosazení mi vyšly zmíněné rovnice. Jinak používám geometrizované jednotky $c = 1, G = 1, k = 1$ .

Vyjádřit pomocí metriky to samozřejmě jde, ale jelikož jsem to nedávno udělal obecně a zabralo mi to půlku A4, myslím, že to dám řešit počítači. :D Díky ještě jednou za rady, asi to vypadá, že to nepůjde jinak, koneckonců jsou to provázané rovnice (Maxwellovy a Einsteinovy) v tuhle chvíli, tak jich bude o něco víc.

Hezký den přeji. :-)
Jimmy

Brzls · 02. 02. 2015 14:01 — Editoval Brzls (02. 02. 2015 14:04)

↑ found:

Tak najít nějaké obecné řešení si jsem jistý že ani nepůjde, je to prostě moc složitý na to aby mělo nějaké analytické řešení.

Nicméně dá se najít spoustu článků o tomto problému. Celkem zajímavé je uvažovat elektrostatický případ. (poslední kapitola zde http://scholarcommons.sc.edu/cgi/viewco … ontext=etd )

Taky by tě možná mohly zajímat Rainich conditions. Je to jedna algebraická a jedna diferenciální podmínka, kterou musí (je nutná i postačující) splňovat Ricciho tenzor aby byl řešením Einstein-Maxwellových rovnic. (zde se zanedbává člen s kosmologickou konstantou).

Na wikkipedii se dá najít soupis nějakých řešení, nicméně prakticky nic o jejich odvození
http://en.wikipedia.org/wiki/Electrovacuum_solution

Nicméně přijde mi že při řešení podobných věcí se postupuje případ od případu jinak.

Matematické Fórum

#1 28. 01. 2015 13:54

D'Alembertův operátor v obecné relativtě

#2 30. 01. 2015 13:03 — Editoval Brzls (30. 01. 2015 17:32)

Re: D'Alembertův operátor v obecné relativtě

#3 30. 01. 2015 19:20 — Editoval found (30. 01. 2015 20:04)

Re: D'Alembertův operátor v obecné relativtě

#4 31. 01. 2015 11:27 — Editoval Brzls (31. 01. 2015 11:28)

Re: D'Alembertův operátor v obecné relativtě

#5 31. 01. 2015 14:24 — Editoval found (31. 01. 2015 14:29)

Re: D'Alembertův operátor v obecné relativtě

#6 02. 02. 2015 14:01 — Editoval Brzls (02. 02. 2015 14:04)

Re: D'Alembertův operátor v obecné relativtě

Zápatí