Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 03. 02. 2015 15:28
Výpočet obsahu pomocí integrálu
Dobrý den,
narazil jsem na tento problém,
jsou dány rovnice křivek:
x=sin(t)
y=cos(t)
S=?
Jak mám vypočíst obsah mezi těmito křivkami? Zkoušel jsem si udělat graf a vyšlo mi to jako obsah v kružnici o poloměru r=1. Ale nevím jak z toho udělat nějaký použitelný vzorec a ten pak správně do podoby  zintegrovat.
zintegrovat.
Děkuji.
Offline
#2 03. 02. 2015 15:45
- Eratosthenes
- Příspěvky: 3110
- Reputace: 140
Re: Výpočet obsahu pomocí integrálu
ahoj ↑ Kallix:,
to nejsou "rovnice křivek" to jsou parametrické rovnice jedné křivky, a sice kružnice. A máš spočítat obsah plochy ohraničené touto křivkou.
Budoucnost patří aluminiu.
Offline
#3 03. 02. 2015 16:04
Re: Výpočet obsahu pomocí integrálu
↑ Eratosthenes:
Ano, ale já nevím jak to vyjádřit pomocí integrálu. A sám jsem napsal, že grafem je kružnice a mám spočítat její obsah. Ale jak k tomu skrze integrál dojdu?
Offline
#4 03. 02. 2015 18:04
- Eratosthenes
- Příspěvky: 3110
- Reputace: 140
Re: Výpočet obsahu pomocí integrálu
↑ Kallix:
musíš vyjádřit y jako funkci x, a pak ve vhodných mezích zintegrovat.
Budoucnost patří aluminiu.
Offline
#6 03. 02. 2015 18:26
- Eratosthenes
- Příspěvky: 3110
- Reputace: 140
Re: Výpočet obsahu pomocí integrálu
↑ Kallix:
postup ↑ Jj: je samozřejmě jednodušší, ale abychom k jeho vztahům dospěli, je potřeba vědět, jak spočítat obsah vymezený parametricky nebo polárně vyjádřenou křivkou.
Budoucnost patří aluminiu.
Offline
#7 03. 02. 2015 18:30
Re: Výpočet obsahu pomocí integrálu
↑ Eratosthenes:
A o to mi právě jde, že nevím jak, nechápu vůbec celé parametrické zadávání. Integrovat normální funkce a počítat z nich nemám problém. A to od Ji: je sice hezké, ale to lze najít na internetu při odvozovaní vzorce pro obsah kružnice.
Offline
#9 03. 02. 2015 19:28
- Eratosthenes
- Příspěvky: 3110
- Reputace: 140
Re: Výpočet obsahu pomocí integrálu
Kallix napsal(a):
... Integrovat normální funkce a počítat z nich nemám problém...
No tady to možná trochu problém bude, integrál té "normální" funkce totiž nebude z nejjednodušších. Tu funkci dostaneš, když se na parametrické vyjádření podíváš jako na soustavu dvou rovnic a vyloučíš z ní parametr t.
Budoucnost patří aluminiu.
Offline
#10 03. 02. 2015 20:51
Re: Výpočet obsahu pomocí integrálu
↑ Eratosthenes:
A mohl by jsi to napsat? Nikdo z mého okolí tomu nerozumí. =(
Offline
#11 03. 02. 2015 22:45
- Eratosthenes
- Příspěvky: 3110
- Reputace: 140
Re: Výpočet obsahu pomocí integrálu
↑ Kallix:
x =sin(t)
y =cos(t)
----------
x^2 =sin^2(t)
y^2 =cos^2(t)
----------
x^2+y^2=1
y =....
Budoucnost patří aluminiu.
Offline
#12 04. 02. 2015 10:37
Re: Výpočet obsahu pomocí integrálu
↑ Kallix:
Tak tedy
1. Máme-li spočítat obsah rovinného obrazce tvaru výseče pak platí:
Je-li hranční křivka dána parametricky: 

2. Pro nás: 
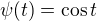

Zbytek je pouze výpočet integrálu![kopírovat do textarea $\int_{0}^{2\pi }\cos ^{2}t dt=[\frac{t}{2}+\frac{\sin 2t}{4}]^{2\pi }_{0}=\frac{2\pi }{2}=\pi $](/mathtex/28/28d09c26f3d8708177002311c4631dfc.gif)
Pokud by poloměr byl  , pak stačí náš výsledek vynásobit výrazem
, pak stačí náš výsledek vynásobit výrazem 
Offline




 rec nebola.
rec nebola.