Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Normála k hyperbole (TOTO TÉMA JE VYŘEŠENÉ)
#1 06. 02. 2015 16:04 — Editoval Callme (06. 02. 2015 16:22)
Normála k hyperbole
Dobry den,
Ako vyriesim nájdite normalovu priamku k hyperbole  tak, aby bola rovnobezna s priamkou
tak, aby bola rovnobezna s priamkou  . Urcte rovnicu normaly a súradnice spolocneho bodu. Mam pouzit diferenciálny pocet reálnej funkcie jednej reálnej premennej bez pouzitia analytickej geometrie.
. Urcte rovnicu normaly a súradnice spolocneho bodu. Mam pouzit diferenciálny pocet reálnej funkcie jednej reálnej premennej bez pouzitia analytickej geometrie.
Cize potrebujem najst dotycnicu ktora je kolma na priamku  .
.
Smernica priamky je 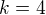 derivaciou rovnice hyperboly dostanem
derivaciou rovnice hyperboly dostanem  zistim suradnice bodu dotyku a nakoniec vyuzijem rovnicu normaly
zistim suradnice bodu dotyku a nakoniec vyuzijem rovnicu normaly  kde
kde  ,
,  ?
?
Offline
- (téma jako vyřešené označil(a) Callme)
#2 06. 02. 2015 22:01
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Normála k hyperbole
Zdravím,
obdobnou úlohu jsi řešil pro elipsu (snad). Přímka  má směrnici
má směrnici  a je to zároveň směrnice normály, kterou hledáš (jelikož musí být k sobě rovnoběžné).
a je to zároveň směrnice normály, kterou hledáš (jelikož musí být k sobě rovnoběžné).
Přes užití derivace rovnice normály je  a koeficient
a koeficient  udává směrnici normály, tedy
udává směrnici normály, tedy  . Odsud najdeš
. Odsud najdeš  a použiješ do
a použiješ do 
To umožní vyjádřit jednu souřadnici, např.  a dosadit do rovnice
a dosadit do rovnice  pro nalezení společného bodu.
pro nalezení společného bodu.
Tak nějak jsi představoval postup? Děkuji.
Offline
#3 06. 02. 2015 22:58
Re: Normála k hyperbole
jelena napsal(a):
Tak nějak jsi představoval postup? Děkuji.
Nie tak ako som napisal ja.
Ked hladam normalu tak to nemam najst vlastne dotycnicu ktora je kolma k priamke  (lebo normala je priamka ktora je kolma na dotycnicu) a to znamena ze
(lebo normala je priamka ktora je kolma na dotycnicu) a to znamena ze 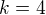 ?
?
Offline
#4 07. 02. 2015 00:08
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Normála k hyperbole
Callme napsal(a):
Smernica priamky je
ano, toto je směrnice přímky kolmé k zadané  a zároveň je to hodnota
a zároveň je to hodnota  (směrnice tečny). Samotnou tečnu hledat nemusíš, jen využíváš tuto hodnotu pro další výpočty
(směrnice tečny). Samotnou tečnu hledat nemusíš, jen využíváš tuto hodnotu pro další výpočty  .
.
Oba využíváme stejnou vlastnost: geometrický význam derivace při sestavení tečny a vztah mezi směrnici tečny a normály. Úlohy jsou si podobné, neměl bys mít problém dořešit i tuto.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Normála k hyperbole (TOTO TÉMA JE VYŘEŠENÉ)