Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 07. 02. 2015 18:37
#5 07. 02. 2015 18:45 — Editoval Freedy (07. 02. 2015 18:45)
Re: Derivácia
↑ vlado_bb:
-.- pozorováním -.-
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#7 07. 02. 2015 18:53
Re: Derivácia
↑ vlado_bb: přesně tak
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#9 07. 02. 2015 21:30 — Editoval Freedy (08. 02. 2015 23:33)
Re: Derivácia
Ahoj,
no, předpokládáš že daný výrok platí libovolné n = k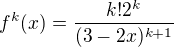
a nyní to dokážeš pro m = k+1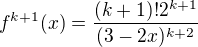
ty potřebuješ dokázat že: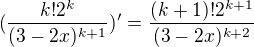
derivujeme samozřejmě podle x takže k je konstanta: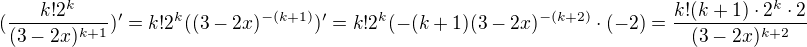
a nyní dosadíme do rovnosti výše:
což je zřejmě přesně to, co jsme dokazovali
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
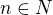 funkcie
funkcie 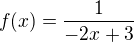
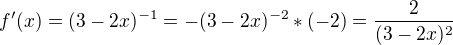
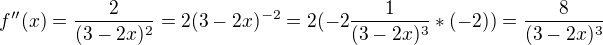
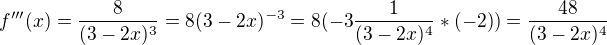
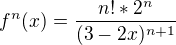 ?
?
 -ta vyzera tak, ako si napisal?
-ta vyzera tak, ako si napisal? .
.
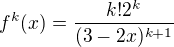
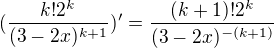 ?
?