Matematické Fórum

maver · 08. 02. 2015 00:28 — Editoval maver (08. 02. 2015 08:22)

Dobrý den, večer ..

Prosím o kontrolu výpočtu. Nevím, jestli mám takto nebo počítat limitu n do nekonečna pro an/bn=1 při bn>0?

//forum.matweb.cz/upload3/img/2015-02/51600_notace.JPG

Brano · 08. 02. 2015 21:17

to zavisi od toho ci je to male o alebo velke O

maver · 08. 02. 2015 22:17

↑ Brano:
to mi nepomohlo :(

Brano · 09. 02. 2015 21:45

ved to ti ani moc nemalo pomoct to bola otazka

je tam male o alebo velke O? lebo to je dost podstatny rozdiel.

maver · 09. 02. 2015 21:53

↑ Brano:
velké

Brano · 10. 02. 2015 11:27

cize ak to chces z definicie, tak potom cez tu nerovnost.

az po 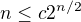$n\le c 2^{n/2}$ si sa dostal spravne a teraz chces najst nejake $c$ pre ktore je to splnene (aspon od nejakeho $n_0$ dalej)
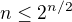no a napriklad pre $c=1$ je nerovnost $n\le 2^{n/2}$ splnena pre vsetky prirodzene cisla okrem $n=3$

cize staci ked dokazes, ze je splnena pre $n>3$ ale na dokazanie nerovnosti ti dosadenie dvoch (alebo aj milion) clenov nestaci
mozes pouzit napr. indukciu, alebo co sa ti paci.

jednoduchsi postup je ale dokazat, ze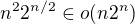

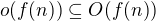$n^22^{n/2}\in o(n2^n)$ lebo $o(f(n))\subseteq O(f(n))$ teda dokaz, ze

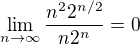$\lim_{n\to\infty}\frac{n^22^{n/2}}{n2^n}=0$ co je dost jednoduche.