Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 26. 02. 2013 11:16
- mysql_dodo

- Zelenáč
- Příspěvky: 15
- Škola: G
- Pozice: student
- Reputace: 0
Telesove uhlopriečky v kvadru.
Zdravim, neviem si vobec rady.
Mam kvader v ktorom:
|AB|= 5 cm, |BC|= 4 cm a |BF|= 6 cm
Mam vypocitat uhol telesovych uhlopriecok...
Dakujem :)
Offline
#2 26. 02. 2013 11:24
Re: Telesove uhlopriečky v kvadru.
↑ mysql_dodo:
Máš trojúhelník ASH, kde S je průsečík úhlopříček. Strany trojúhelníka spočítáš z Pyth. věty. a pak použiješ např. kosínovou větu pro úhel u vrcholu S
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#3 26. 02. 2013 12:12 — Editoval mysql_dodo (26. 02. 2013 12:19)
- mysql_dodo

- Zelenáč
- Příspěvky: 15
- Škola: G
- Pozice: student
- Reputace: 0
Re: Telesove uhlopriečky v kvadru.
sorac zabudol som dodat že, Uhol medzi BH a EC...
to vlastne pouzijem trojuholnik ESH vsak? :)
Dakujem uz mi to vyslo krasne... 54, 24 stupnov
Offline
#5 18. 02. 2015 12:34
- Marek Korman

- Zelenáč
- Příspěvky: 9
- Reputace: 0
Re: Telesove uhlopriečky v kvadru.
↑ mysql_dodo:
Prosím ťa mohol by si mi poslať nejaky´jedonuchy navod ako si to vypočital,neviem ani za pána prísť na ten vysledok ...vdaka moc kámo.
Offline
#6 18. 02. 2015 13:52
Re: Telesove uhlopriečky v kvadru.
Princip řešení:
Mějme kvádr s rozměry 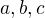 . (Načrtnšte si obrázek.)
. (Načrtnšte si obrázek.)
Dvě hrany  vycházející z téhož vrcholu kvádru jsou navzájem kolmé, tedy jsou odvěsnami jistého
vycházející z téhož vrcholu kvádru jsou navzájem kolmé, tedy jsou odvěsnami jistého
pravoúhlého trojúhelníka s přeponou  (ta je jednou ze stěnových úhlopříček kvádru). Tento trojúhelník
(ta je jednou ze stěnových úhlopříček kvádru). Tento trojúhelník
leží v jisté rovíně  .
.
Vezměme některý z krajních bodů úsečky  . Z něho vychází jedna z hran kvádru délky
. Z něho vychází jedna z hran kvádru délky  , ta je kolmá
, ta je kolmá
k rovině  a tedy i k úsečce
a tedy i k úsečce  . Tyto úsečky o délkách
. Tyto úsečky o délkách 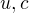 jsou odvěsnami jiného pravoúhlého trojúhelníka,
jsou odvěsnami jiného pravoúhlého trojúhelníka,
jehož přeponou je tělesová úhlopříčka daného kváru.
Tělesovou úhlopříčku kvádru tedy spočteme z jeho rozměrů dvojím použitím Pythagorovy věty.
Offline
#7 18. 02. 2015 14:59
- Marek Korman

- Zelenáč
- Příspěvky: 9
- Reputace: 0
Re: Telesove uhlopriečky v kvadru.
↑ Rumburak:
Tak som vypočital stenovu uhlopriečku u=6,403 následne som to dosadil do druhej pyth.vety a vypočital dlžku telesovej uhl. u1=8,77496 ..čo s s tym dalej ? tuto uhl. som predelil 2 a dostal som 4,387 ...mam tuto hodnotu spolu s dlžkou BC dosadiť do cosinusovej vety ??
Offline
#8 18. 02. 2015 15:18 — Editoval Rumburak (20. 02. 2015 09:39)
Re: Telesove uhlopriečky v kvadru.
↑ Marek Korman:
Jo pardon, přehlédl jsem, že je požadováno vypočítat úhel tělesových úhlopříček.
Ano, lze použít kosinovou větu na zvolený rovnoramenný trojúhelník, jehož rameny jsou poloviny
zvolených tělesových úhlpopříček.
Máme zde čtyři volby s dvěma různými výsledky.
Toto je také špatně, musel jsem včera mít vlčí mlhu, omlouvám se.
Uvažujme libovolnou stěnu onoho kvádru, třeba stěnu 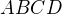 (při cyklickém označení), kde úsečky
(při cyklickém označení), kde úsečky  jsou hrany kvádru, avšak volba stěny není podstatná. Při tom platí:
jsou hrany kvádru, avšak volba stěny není podstatná. Při tom platí:
a) každý z bodů  je jedním z krajních bodů některé (a sice právě jedné) z tělesových úklopříček kvádru ,
je jedním z krajních bodů některé (a sice právě jedné) z tělesových úklopříček kvádru ,
b) každá z tělesových úhlopříček kvádru má dva krajní body, z nichž právě jeden je některý z bodů  .
.
Stručně řečeno: body  odpovídají jednotlivým tělesovým úhlopříčkám a naopak. Označme
odpovídají jednotlivým tělesovým úhlopříčkám a naopak. Označme  tělesové úhlopříčky odpovídající po řadě svým bodům
tělesové úhlopříčky odpovídající po řadě svým bodům  .
.
Je potřeba zjistit
1. vzájemnou odchylku 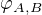 přímek
přímek  , která bude stejná jako odchylka přímek
, která bude stejná jako odchylka přímek  ,
,
2. vzájemnou odchylku 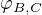 přímek
přímek  , která bude stejná jako odchylka přímek
, která bude stejná jako odchylka přímek  ,
,
3. vzájemnou odchylku  přímek
přímek  , která bude stejná jako odchylka přímek
, která bude stejná jako odchylka přímek  .
.
Všechny tělesové úhlopříčky mají společný ptůsečík  (střed kvádru) a tutéž délku
(střed kvádru) a tutéž délku  ,
,
kde 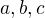 jsou rozměry kvádru a
jsou rozměry kvádru a  je společná vzdálenost bodu
je společná vzdálenost bodu  od vrcholů kvádru.
od vrcholů kvádru.
Pomocí cosinové věty dostáváme rovnice
 ,
,
 ,
,
 .
.
Vyjde-li některý z úhlů tupý, zpravidla ho v závěru nahrazujeme jeho doplňkem do úhlu přímého.
Offline
#9 18. 02. 2015 15:26
- Marek Korman

- Zelenáč
- Příspěvky: 9
- Reputace: 0
Re: Telesove uhlopriečky v kvadru.
Ulohou je vypočitať uhol medzi telesovymi uhlopriečkami ...
Offline
#10 18. 02. 2015 15:36 — Editoval Rumburak (18. 02. 2015 15:40)
#11 18. 02. 2015 15:48
- Marek Korman

- Zelenáč
- Příspěvky: 9
- Reputace: 0
Re: Telesove uhlopriečky v kvadru.
↑ Rumburak:
Ked dosadim vypočitane hodnoty nechcem mi vobec vyjsť dany uhol ..
Offline
#12 19. 02. 2015 11:54
Re: Telesove uhlopriečky v kvadru.
↑ Marek Korman:
Příspěvek ↑ Rumburak: jsem ještě musel přepracovat.
Případně sem napiš nesprávně vycházející výpočet a zkontrolujeme ho.
Offline
#13 19. 02. 2015 12:59
- Marek Korman

- Zelenáč
- Příspěvky: 9
- Reputace: 0
Re: Telesove uhlopriečky v kvadru.


neviem kde robím chybu,ospravedlnujem za za kvalitu písma,mám zlomenu ruku tak píšem ľavou :)
Offline
#14 19. 02. 2015 13:44 — Editoval gadgetka (19. 02. 2015 14:27)
Re: Telesove uhlopriečky v kvadru.
Řekla bych, že máš řešit trojúhelník ASE, odchylka leží u středu S a délka AE je 6 cm, nikoli 4.
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#15 19. 02. 2015 14:12 — Editoval Marek Korman (19. 02. 2015 14:16)
- Marek Korman

- Zelenáč
- Příspěvky: 9
- Reputace: 0
Re: Telesove uhlopriečky v kvadru.
Odkial ste prosim Vás dostali hodnoty 41/4 a 77/4 ??
Offline
#16 19. 02. 2015 14:31
Re: Telesove uhlopriečky v kvadru.
Děkuji za dotaz. Díky němu jsem našla chybu, kterou jsem v předchozím textu opravila. Ale abych odpověděla. Nepřeváděla jsem odmocniny na desetinná místa. Podstavná úhlopříčka: 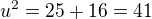
Tělesová úhlopříčka 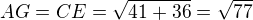
odtud 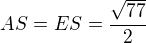
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#17 19. 02. 2015 14:43
- Marek Korman

- Zelenáč
- Příspěvky: 9
- Reputace: 0
Re: Telesove uhlopriečky v kvadru.
Dakujem,áno tomuto rozumiem,no ešte stále nechápem prečo do kosin.vety dosadzujete za premenne a,b hodnotu 77/4 ...
Offline
#18 19. 02. 2015 14:45
Re: Telesove uhlopriečky v kvadru.
AS a ES má poloviční rozměr tělesové úhlopříčky. Když tedy ten rozměr umocňuji na druhou, dostanu
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#19 19. 02. 2015 14:46
Re: Telesove uhlopriečky v kvadru.
↑ Marek Korman:
Počítáme tedy odchylku úseček  , takže použijeme rovnici
, takže použijeme rovnici
 ,
,
do níž dosadíme  . Tedy
. Tedy  ,
,
pomocí webové kalkulačky  , tedy něco přes
, tedy něco přes 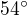 , pokud jsem
, pokud jsem
nezmáčkl někde špatný knoflík.
Offline
